Tứ giác nội tiếp là một khái niệm quan trọng trong hình học, đặc biệt là khi giải các bài toán liên quan đến đường tròn. Hiểu rõ về định nghĩa, tính chất và các dấu hiệu nhận biết tứ giác nội tiếp là chìa khóa để giải quyết nhiều bài toán hình học một cách hiệu quả. Bài viết này sẽ cung cấp một cái nhìn toàn diện về tứ giác nội tiếp, tập trung vào các tính chất quan trọng và ứng dụng của chúng.
1. Định Nghĩa Tứ Giác Nội Tiếp
Tứ giác nội tiếp (hay còn gọi là tứ giác nội tiếp đường tròn) là tứ giác có tất cả bốn đỉnh cùng nằm trên một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp tứ giác.
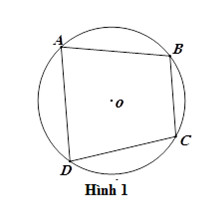Tứ giác ABCD nội tiếp đường tròn tâm O
Hình ảnh minh họa tứ giác ABCD nội tiếp đường tròn (O). Alt: Tứ giác nội tiếp ABCD với các đỉnh nằm trên đường tròn tâm O, minh họa khái niệm tứ giác nội tiếp.
Ví dụ: Trong hình trên, tứ giác (ABCD) nội tiếp đường tròn (left( O right)), và đường tròn (left( O right)) ngoại tiếp tứ giác (ABCD).
2. Định Lý Về Tứ Giác Nội Tiếp
Định lý quan trọng nhất liên quan đến tứ giác nội tiếp là:
- Định lý 1: Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng (180^circ ).
- Định lý 2: Nếu một tứ giác có tổng số đo hai góc đối diện bằng (180^circ ) thì tứ giác đó nội tiếp được đường tròn.
Ví dụ: Trong tứ giác nội tiếp (ABCD), ta có:
- (widehat A + widehat C = 180^circ )
- (widehat B + widehat D = 180^circ )
3. Các Dấu Hiệu Nhận Biết Tứ Giác Nội Tiếp
Để chứng minh một tứ giác là nội tiếp, ta có thể sử dụng một trong các dấu hiệu sau:
- Dấu hiệu 1: Tứ giác có tổng hai góc đối bằng (180^circ ).
- Dấu hiệu 2: Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
- Dấu hiệu 3: Tứ giác có bốn đỉnh cách đều một điểm (điểm này là tâm đường tròn ngoại tiếp tứ giác).
- Dấu hiệu 4: Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc (alpha ) (cùng nhìn cạnh đó dưới một góc không đổi).
4. Ứng Dụng của Tính Chất Tứ Giác Nội Tiếp
Tính Chất Của Tứ Giác Nội Tiếp được sử dụng rộng rãi trong giải toán hình học, đặc biệt là trong các bài toán liên quan đến:
- Chứng minh tứ giác nội tiếp: Áp dụng các dấu hiệu nhận biết nêu trên.
- Chứng minh các góc bằng nhau: Sử dụng tính chất góc nội tiếp cùng chắn một cung.
- Chứng minh các đường thẳng song song: Sử dụng tính chất các góc so le trong, đồng vị bằng nhau.
- Chứng minh các hệ thức hình học: Sử dụng định lý Ptolemy hoặc các hệ thức lượng trong tam giác.
- Tìm quỹ tích điểm: Dựa vào tính chất góc nhìn của các điểm trên đường tròn.
Ví dụ về cách chứng minh tứ giác nội tiếp:
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Chứng minh tứ giác BFEC nội tiếp.
- Giải: Vì BE là đường cao nên (widehat{BEC} = 90^circ). Vì CF là đường cao nên (widehat{BFC} = 90^circ). Suy ra (widehat{BEC} + (widehat{BFC} = 180^circ). Vậy tứ giác BFEC nội tiếp (tứ giác có tổng hai góc đối bằng 180 độ).
5. Các Hình Đặc Biệt Nội Tiếp Đường Tròn
Một số hình đặc biệt luôn nội tiếp được đường tròn:
- Hình chữ nhật
- Hình vuông
- Hình thang cân
Lưu ý: Hình bình hành và hình thoi không nội tiếp được đường tròn, trừ khi chúng là hình chữ nhật hoặc hình vuông.
Hiểu và vận dụng linh hoạt các tính chất của tứ giác nội tiếp là một kỹ năng quan trọng trong giải toán hình học. Việc nắm vững định nghĩa, các dấu hiệu nhận biết và các ứng dụng của tứ giác nội tiếp sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và chính xác.
