Để làm chủ các bài toán liên quan đến Tính Arctan, chúng ta cần hiểu rõ về hàm số y = arctan x. Bài viết này sẽ cung cấp một cái nhìn toàn diện về định nghĩa, đồ thị, các quy tắc và công thức liên quan đến tính arctan, giúp bạn tự tin giải quyết mọi bài tập.
Định nghĩa hàm Arctan
Hàm số y = arctan x, hay còn gọi là hàm arctangent, là hàm ngược của hàm tang. Nó trả về góc mà có giá trị tang bằng x. Về mặt toán học, arctan x là giá trị y sao cho tan(y) = x, với y nằm trong khoảng (-π/2, π/2). Nói cách khác, nếu tan y = x thì y = arctan x.
Ví dụ: arctan(1) = π/4 (hoặc 45°) vì tan(π/4) = 1.
Đồ thị hàm số Arctan và tính chất
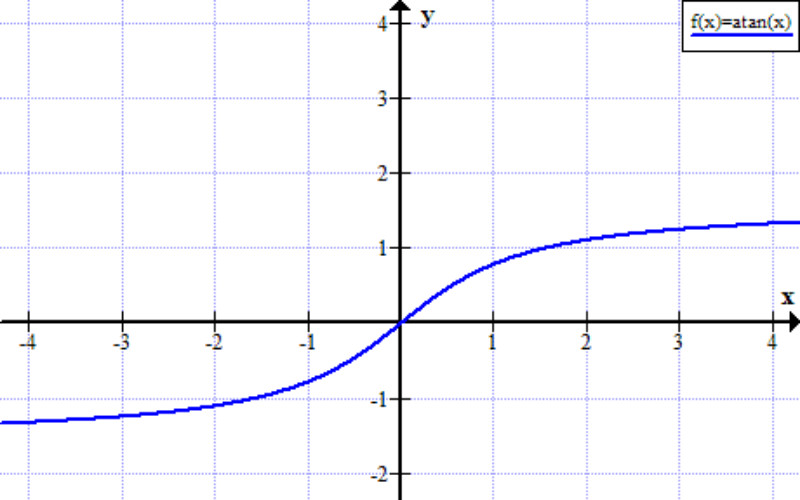
Đồ thị của hàm số y = arctan x có dạng một đường cong đối xứng qua gốc tọa độ. Nó nằm ở góc phần tư thứ nhất và thứ ba.
- Miền xác định: Tập hợp tất cả các số thực R.
- Tập giá trị: Khoảng (-π/2, π/2).
- Tính đơn điệu: Hàm số arctan x đồng biến trên toàn bộ miền xác định.
- Tính liên tục: Hàm số arctan x liên tục trên toàn bộ miền xác định.
- Tiệm cận: Đồ thị hàm số có hai đường tiệm cận ngang là y = π/2 và y = -π/2. Điều này có nghĩa là khi x tiến tới vô cực dương, arctan x tiến tới π/2; và khi x tiến tới vô cực âm, arctan x tiến tới -π/2.
Các quy tắc và công thức quan trọng khi tính Arctan
Việc nắm vững các quy tắc và công thức sau là chìa khóa để giải quyết các bài toán liên quan đến tính arctan:
| Công thức | Diễn giải |
|---|---|
| tan(arctan x) = x | Hàm tang của arctan x luôn bằng x. |
| arctan(-x) = -arctan x | Hàm arctan là hàm lẻ. |
| arctan α + arctan β = arctan [ ( α + β ) / (1- αβ ) ] | Công thức cộng arctan, sử dụng khi tính arctan của tổng hai số. |
| arctan α – arctan β = arctan [ ( α – β ) / (1+ αβ ) ] | Công thức trừ arctan, sử dụng khi tính arctan của hiệu hai số. |
| sin ( arctan x ) = x/√(1 + x²) | Biểu diễn sin của arctan x theo x. |
| cos ( arctan x ) = 1/√(1 + x²) | Biểu diễn cos của arctan x theo x. |
| arctan x = arcsin x/√(x² + 1) | Liên hệ giữa arctan và arcsin. |
| (arctan x)’ = 1/(1 + x²) | Đạo hàm của hàm arctan x. Đây là công thức cực kỳ quan trọng trong giải tích. |
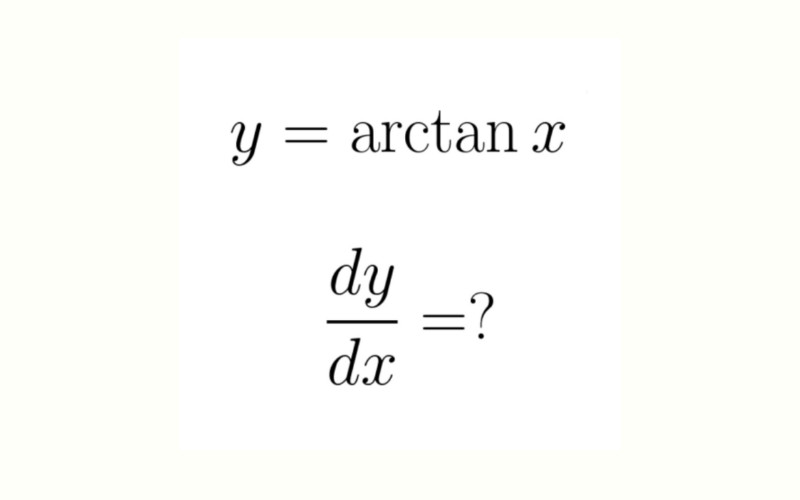
Đạo hàm của hàm số Arctan
Đạo hàm của hàm số y = arctan x là một kiến thức then chốt trong giải tích. Công thức đạo hàm của arctan x là:
(arctan x)’ = 1/(1 + x²)
Công thức này được sử dụng rộng rãi trong việc tính tích phân, tìm cực trị và giải các bài toán liên quan đến tốc độ thay đổi.
Để chứng minh công thức này, ta sử dụng phương pháp lấy đạo hàm hàm ẩn:
- Đặt y = arctan x => tan y = x
- Lấy đạo hàm cả hai vế theo x: (tan y)’ = x’ => (1 + tan²y) * y’ = 1
- Suy ra: y’ = 1 / (1 + tan²y) = 1 / (1 + x²)
Ứng dụng của hàm số Arctan
Hàm số arctan không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:
- Vật lý: Tính góc bắn trong chuyển động ném xiên, xác định góc lệch trong các bài toán quang học.
- Kỹ thuật: Xử lý tín hiệu, thiết kế bộ điều khiển, tính toán góc trong các hệ thống cơ khí.
- Khoa học máy tính: Xử lý ảnh, đồ họa máy tính, machine learning.
- Địa lý: Tính toán khoảng cách và phương hướng trên bản đồ.
Bài tập tự luyện về tính Arctan
Để củng cố kiến thức và kỹ năng, bạn nên tự luyện các dạng bài tập sau:
- Tính giá trị của arctan tại các điểm khác nhau (ví dụ: arctan(0), arctan(-1), arctan(√3)).
- Tìm đạo hàm của các hàm số chứa arctan (ví dụ: y = arctan(x²), y = x * arctan(x)).
- Giải các phương trình lượng giác chứa arctan.
- Áp dụng kiến thức về arctan để giải các bài toán thực tế (ví dụ: tính góc bắn để đạt tầm xa tối đa trong chuyển động ném xiên).
Hiểu rõ về tính arctan, từ định nghĩa đến ứng dụng thực tế, sẽ giúp bạn tự tin chinh phục các bài toán toán học và khám phá thế giới xung quanh một cách sâu sắc hơn.

