Định nghĩa tích của một số với một vectơ
Cho số thực $k$ khác 0 và vectơ $vec{a}$ khác vectơ $vec{0}$. Tích của số $k$ với vectơ $vec{a}$, ký hiệu là $kvec{a}$, là một vectơ:
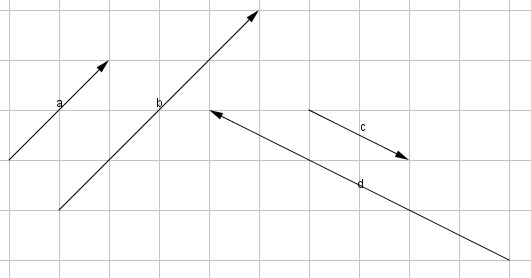
- Cùng hướng với $vec{a}$ nếu $k > 0$.
- Ngược hướng với $vec{a}$ nếu $k < 0$.
- Độ dài bằng $|k||vec{a}|$.
Quy ước:
- $0vec{a} = vec{0}$
- $kvec{0} = vec{0}$
Tính chất của tích một số với một vectơ
Tích của một số với một vectơ có các tính chất sau:
-
Tính phân phối đối với phép cộng vectơ:
$k(vec{m} + vec{n}) = kvec{m} + kvec{n}$
-
Tính phân phối đối với phép cộng các số:
$(a + b)vec{x} = avec{x} + bvec{x}$
-
Tính kết hợp:
$a(bvec{c}) = (ab)vec{c}$
-
Tính chất đơn vị và đối:
- $1vec{a} = vec{a}$
- $(-1)vec{a} = -vec{a}$
-
Điều kiện bằng vectơ không:
$kvec{a} = vec{0} Leftrightarrow k = 0$ hoặc $vec{a} = vec{0}$
Ứng dụng:
-
Nếu $E$ là trung điểm của đoạn thẳng $MN$ thì với mọi điểm $I$, ta có:
$vec{IM} + vec{IN} = 2vec{IE}$
-
Nếu $U$ là trọng tâm tam giác $NCT$ thì với mọi điểm $I$ ta có:
$vec{IN} + vec{IC} + vec{IT} = 3vec{IU}$
Điều kiện để hai vectơ cùng phương
- Điều kiện cần và đủ để vectơ $vec{a}$ và vectơ $vec{b}$ ($vec{b} neq vec{0}$) cùng phương là tồn tại một số $k$ sao cho $vec{a} = kvec{b}$.
- Ba điểm phân biệt $M$, $N$, $O$ thẳng hàng khi và chỉ khi có số $k neq 0$ để $vec{MN} = kvec{MO}$.
Phân tích một vectơ thành hai vectơ không cùng phương
Cho hai vectơ $vec{a}$ và $vec{b}$ không cùng phương. Khi đó, mọi vectơ $vec{k}$ đều có thể biểu diễn một cách duy nhất theo hai vectơ $vec{a}$, $vec{b}$: $vec{k} = mvec{a} + nvec{b}$, trong đó $m$, $n$ là các số thực duy nhất.
Bài tập áp dụng về tích của một số với một vectơ
Tính độ dài vectơ
Phương pháp giải: Sử dụng định nghĩa, các quy tắc cộng, trừ vectơ, kết hợp với định lý Pytago, hệ thức lượng trong tam giác.
Ví dụ 1: Tam giác $ABC$ đều cạnh $a$, $M$ là trung điểm $BC$. Dựng và tính độ dài các vectơ sau:
a) $vec{MA} + frac{1}{2}vec{CB}$
b) $vec{BA} – frac{1}{2}vec{BC}$
Lời giải:
a) Ta có: $frac{1}{2}vec{CB} = vec{CM}$
Theo quy tắc ba điểm:
$frac{1}{2}vec{CB} + vec{MA} = vec{CM} + vec{MA} = vec{CA}$
Vậy: $|frac{1}{2}vec{CB} + vec{MA}| = |vec{CA}| = a$
b) Vì $vec{BM} = frac{1}{2}vec{BC}$ nên theo quy tắc trừ:
$vec{BA} – frac{1}{2}vec{BC} = vec{BA} – vec{BM} = vec{MA}$
Áp dụng định lý Pytago: $MA = sqrt{AB^2 – BM^2} = sqrt{a^2 – (frac{a}{2})^2} = frac{asqrt{3}}{2}$
Vậy: $|vec{BA} – frac{1}{2}vec{BC}| = |vec{MA}| = frac{asqrt{3}}{2}$
Ví dụ 2: Cho hình vuông $ABCD$ cạnh $a$.
a) Chứng minh rằng $vec{u} = 4vec{MA} – 3vec{MB} + vec{MC} – 2vec{MD}$ không phụ thuộc vào vị trí của điểm $M$.
b) Tính $|vec{u}|$.
Lời giải:
a) Gọi $O$ là tâm hình vuông $ABCD$. Áp dụng quy tắc ba điểm:
$vec{u} = 4(vec{MO} + vec{OA}) – 3(vec{MO} + vec{OB}) + (vec{MO} + vec{OC}) – 2(vec{MO} + vec{OD}) = 4vec{OA} – 3vec{OB} + vec{OC} – 2vec{OD}$
Mà $vec{OD} = -vec{OB}$, $vec{OC} = -vec{OA}$ nên $vec{u} = 3vec{OA} – vec{OB}$.
Vậy, $vec{u}$ không phụ thuộc vào vị trí của $M$.
b) Chọn $A’$ trên tia $OA$ sao cho $OA’ = 3OA$.
Khi đó: $vec{OA’} = 3vec{OA} Rightarrow vec{u} = vec{OA’} – vec{OB} = vec{BA’}$
Mặt khác: $BA’ = sqrt{OB^2 + (OA’)^2} = sqrt{OB^2 + 9OA^2} = asqrt{5} Rightarrow |vec{u}| = asqrt{5}$.
Tìm điểm thỏa mãn đẳng thức vectơ
Phương pháp giải:
- Biến đổi đẳng thức vectơ về dạng $vec{AN} = vec{a}$, trong đó $A$ và $vec{a}$ đã biết.
- Biến đổi về đẳng thức vectơ của trọng tâm tam giác và trung điểm đoạn thẳng.
Ví dụ 1: Cho tứ giác $ABCD$. Tìm các điểm $M$, $N$, $P$ sao cho:
a) $2vec{MA} + vec{MB} + vec{MC} = vec{0}$
b) $vec{NA} + vec{NB} + vec{NC} + vec{ND} = vec{0}$
Lời giải:
a) Gọi $I$ là trung điểm của $BC Rightarrow vec{MB} + vec{MC} = 2vec{MI}$.
Do đó: $2vec{MA} + vec{MB} + vec{MC} = vec{0} Leftrightarrow 2vec{MA} + 2vec{MI} = vec{0} Leftrightarrow vec{MA} + vec{MI} = vec{0}$.
Vậy $M$ là trung điểm $AI$.
b) Gọi $K$, $H$ là trung điểm của $AB$, $CD$. Ta có:
$vec{NA} + vec{NB} + vec{NC} + vec{ND} = vec{0} Leftrightarrow 2vec{NK} + 2vec{NH} = vec{0}$.
Vậy $N$ là trung điểm $KH$.
Chứng minh đẳng thức vectơ
Phương pháp giải: Áp dụng các tính chất vectơ, quy tắc ba điểm, quy tắc hình bình hành, phép trừ vectơ, tính chất trung điểm, trọng tâm.
Ví dụ 1: Cho tứ giác $ABCD$. $I$, $J$ là trung điểm $AB$, $CD$; $O$ là trung điểm $IJ$. Chứng minh:
- $vec{BD} + vec{AC} = 2vec{IJ}$
- $vec{OA} + vec{OB} + vec{OC} + vec{OD} = vec{0}$