Trong chương trình hình học không gian, khái niệm về vật tròn xoay và thể tích của chúng đóng vai trò quan trọng. Bài viết này sẽ đi sâu vào các công thức tính Thể Tích Vật Tròn Xoay, kèm theo các ví dụ minh họa và bài tập ứng dụng từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
Vật Tròn Xoay Là Gì?
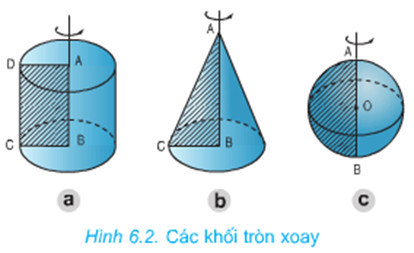
Vật tròn xoay được tạo thành khi quay một hình phẳng quanh một trục cố định. Các hình tròn xoay thường gặp bao gồm hình nón, hình cầu và hình trụ. Việc tính thể tích của những hình này có ứng dụng rộng rãi trong thực tế, từ xây dựng đến thiết kế.
Hình ảnh minh họa các dạng vật tròn xoay thường gặp như hình cầu, hình trụ và hình nón, giúp người đọc dễ hình dung khái niệm.
Thể tích của vật tròn xoay là lượng không gian mà vật đó chiếm giữ. Việc tính toán thể tích này dựa trên các công thức tích phân, tùy thuộc vào trục quay và hình dạng của mặt phẳng được quay.
Công Thức Tính Thể Tích Vật Tròn Xoay Quanh Trục Ox
Xét trường hợp hình phẳng giới hạn bởi các đường sau:
- Đường cong y = f(x)
- Trục hoành y = 0
- Hai đường thẳng x = a và x = b
Khi đó, thể tích vật tròn xoay tạo thành khi quay hình phẳng này quanh trục Ox được tính bằng công thức:
Nếu hình phẳng giới hạn bởi hai đường cong y = f(x) và y = g(x) (với g(x) ≤ f(x) ∀ x ∈ [a, b]), trục Ox và hai đường thẳng x = a và x = b, thì thể tích vật tròn xoay được tính như sau:
Công Thức Tính Thể Tích Vật Tròn Xoay Quanh Trục Oy
Tương tự, để tính thể tích vật tròn xoay khi quay quanh trục Oy, ta xét các trường hợp sau:
Trường hợp 1: Hình phẳng giới hạn bởi đường cong x = g(y), trục tung x = 0, và hai đường thẳng y = c và y = d.
Thể tích vật tròn xoay được tính bằng:
Trường hợp 2: Hình phẳng giới hạn bởi hai đường cong x = f(y) và x = g(y) (với g(y) ≤ f(y) ∀ y ∈ [c, d]), trục Oy và hai đường thẳng y = c và y = d.
Thể tích vật tròn xoay được tính bằng:
Ví Dụ Minh Họa và Bài Tập Ứng Dụng
Để hiểu rõ hơn về cách áp dụng các công thức trên, chúng ta sẽ xét một số ví dụ cụ thể:
Ví dụ 1: Tính thể tích vật tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường cong y = 1 – x², trục Ox, và hai đường thẳng x = 0 và x = 1 quanh trục Ox.
Giải:
Áp dụng công thức thể tích vật tròn xoay quanh trục Ox:
Thể tích vật tròn xoay là:
Hình ảnh minh họa các bước giải chi tiết cho ví dụ tính thể tích vật tròn xoay quanh trục Ox, giúp người đọc dễ dàng theo dõi và áp dụng.
Ví dụ 2: Tính thể tích vật tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường cong x = 2/y, trục Oy, và hai đường thẳng y = 1 và y = 4 quanh trục Oy.
Hình ảnh minh họa cách giải bài toán thể tích vật tròn xoay quanh trục Oy, giúp người học nắm bắt phương pháp.
Ví dụ 3: Tính thể tích vật tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường cong y = √x, y = -x + 2, và y = 0 quanh trục Oy.
Hình ảnh minh họa việc tính toán thể tích vật tròn xoay khi quay quanh trục Oy với các đường cong phức tạp hơn, yêu cầu phân tích kỹ lưỡng.
Ví dụ 4: Cho hình phẳng (H) giới hạn bởi đồ thị hàm số , trục Ox và đường thẳng x = 1. Tính thể tích vật tròn xoay thu được khi quay (H) quanh trục Ox.
Ví dụ 5: Thể tích V của vật tròn xoay được tạo thành bằng cách quay quanh hình phẳng được giới hạn bằng các đường , y = 0, x = 4 và trục Ox. Đường thẳng x = a (0 tại M.
Gọi V1 là thể tích vật tròn xoay được tạo thành khi quay tam giác MOH quanh trục Ox. Biết rằng V = 2V1. Tính a?
Kết Luận
Việc nắm vững công thức và phương pháp tính thể tích vật tròn xoay là rất quan trọng trong chương trình toán học phổ thông. Hy vọng qua bài viết này, bạn đã có cái nhìn tổng quan và chi tiết về chủ đề này, từ đó tự tin giải quyết các bài tập và ứng dụng vào thực tế. Hãy luyện tập thêm nhiều bài tập khác nhau để củng cố kiến thức và nâng cao kỹ năng giải toán.