Phương trình sinx = 1/2 là một trong những dạng toán lượng giác cơ bản và quan trọng. Bài viết này sẽ đi sâu vào cách giải phương trình này, cung cấp kiến thức nền tảng và các ví dụ minh họa để bạn có thể nắm vững phương pháp giải.
Giá Trị Lượng Giác Đặc Biệt
Trước khi đi vào giải phương trình, chúng ta cần nắm vững các giá trị lượng giác đặc biệt của một số góc thường gặp:
- sin(π/6) = sin(30°) = 1/2
- cos(π/3) = cos(60°) = 1/2
- tan(π/4) = tan(45°) = 1
Những giá trị này sẽ giúp chúng ta tìm ra nghiệm của phương trình sinx = 1/2 một cách nhanh chóng.
Giải Phương Trình sinx = 1/2
Phương trình sinx = 1/2 có nghĩa là chúng ta cần tìm tất cả các góc x sao cho sin của góc đó bằng 1/2.
Sử Dụng Đường Tròn Lượng Giác
Đường tròn lượng giác là công cụ trực quan giúp chúng ta hiểu rõ hơn về hàm sin. Trên đường tròn lượng giác, sin của một góc được biểu diễn bằng tung độ của điểm trên đường tròn tương ứng với góc đó.
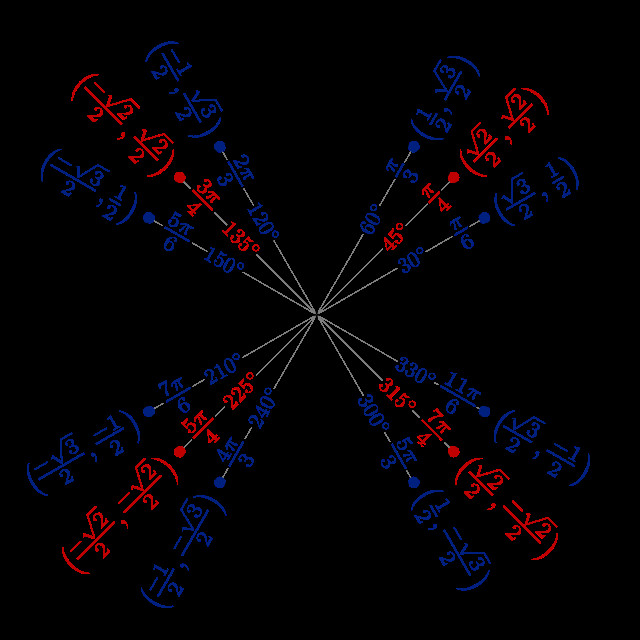Đường tròn lượng giác minh họa giá trị sin x = 1/2
Alt text: Đường tròn lượng giác với góc pi/6 và 5pi/6 có sin bằng 1/2, minh họa nghiệm của phương trình sinx = 1/2.
Nhìn vào đường tròn lượng giác, ta thấy có hai điểm trên đường tròn có tung độ bằng 1/2. Hai điểm này tương ứng với hai góc là π/6 (30°) và 5π/6 (150°).
Nghiệm Tổng Quát
Vì hàm sin là hàm tuần hoàn với chu kỳ 2π, nên nếu x là một nghiệm của phương trình sinx = 1/2, thì x + k2π cũng là một nghiệm, với k là một số nguyên bất kỳ.
Do đó, nghiệm tổng quát của phương trình sinx = 1/2 là:
- x = π/6 + k2π
- x = 5π/6 + k2π
Với k ∈ Z (k là một số nguyên).
Các Bước Giải Phương Trình sinx = 1/2
Để giải phương trình sinx = 1/2, bạn có thể làm theo các bước sau:
- Xác định giá trị sin cơ bản: Tìm một góc α sao cho sin(α) = 1/2. Trong trường hợp này, α = π/6.
- Tìm nghiệm thứ hai: Sử dụng tính chất sin(π – α) = sin(α) để tìm nghiệm thứ hai. Trong trường hợp này, π – π/6 = 5π/6.
- Viết nghiệm tổng quát: Thêm k2π vào cả hai nghiệm để biểu diễn tất cả các nghiệm của phương trình.
Ví Dụ Minh Họa
Ví dụ 1: Giải phương trình sinx = 1/2 trên khoảng [0; 2π].
Giải:
- Nghiệm cơ bản: x = π/6
- Nghiệm thứ hai: x = 5π/6
- Vì cả hai nghiệm này đều nằm trong khoảng [0; 2π], nên tập nghiệm của phương trình là {π/6; 5π/6}.
Ví dụ 2: Giải phương trình sin(2x) = 1/2.
Giải:
- Đặt t = 2x. Khi đó, phương trình trở thành sin(t) = 1/2.
- Nghiệm của phương trình sin(t) = 1/2 là:
- t = π/6 + k2π
- t = 5π/6 + k2π
- Thay t = 2x, ta có:
- 2x = π/6 + k2π => x = π/12 + kπ
- 2x = 5π/6 + k2π => x = 5π/12 + kπ
Vậy nghiệm của phương trình sin(2x) = 1/2 là x = π/12 + kπ và x = 5π/12 + kπ, với k ∈ Z.
Ứng Dụng Của Phương Trình sinx = 1/2
Phương trình sinx = 1/2 không chỉ là một bài toán lượng giác đơn thuần, mà còn có nhiều ứng dụng trong thực tế, ví dụ như:
- Vật lý: Tính toán quỹ đạo của vật thể chuyển động theo hình sin.
- Kỹ thuật: Thiết kế mạch điện xoay chiều.
- Âm nhạc: Phân tích sóng âm.
Alt text: Đồ thị sóng sin minh họa dao động điều hòa, một ứng dụng của hàm sin trong vật lý và kỹ thuật, liên quan đến việc giải phương trình lượng giác.
Kết Luận
Hiểu rõ cách giải phương trình sinx = 1/2 là nền tảng quan trọng để giải các bài toán lượng giác phức tạp hơn. Hy vọng rằng bài viết này đã cung cấp cho bạn kiến thức và kỹ năng cần thiết để tự tin giải quyết các bài toán liên quan đến sinx = 1/2. Hãy luyện tập thêm nhiều ví dụ để nắm vững kiến thức này!
