1. Lý Thuyết Cơ Bản về Góc Giữa Đường Thẳng và Mặt Phẳng
Để nắm vững cách tính góc giữa đường thẳng và mặt phẳng, trước tiên chúng ta cần hiểu rõ định nghĩa và các ký hiệu liên quan. Góc giữa đường thẳng và mặt phẳng là một khái niệm quan trọng trong hình học không gian, thường xuất hiện trong các bài toán liên quan đến khối đa diện và tính toán khoảng cách.
1.1. Định Nghĩa Góc Giữa Đường Thẳng và Mặt Phẳng
Có hai trường hợp chính cần xem xét:
- Trường hợp 1: Nếu đường thẳng vuông góc với mặt phẳng, góc giữa chúng được định nghĩa là 90 độ.
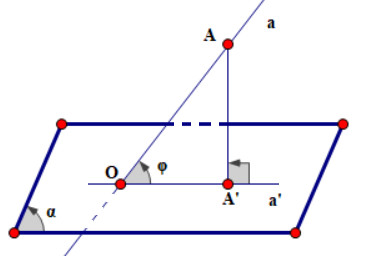
- Trường hợp 2: Nếu đường thẳng không vuông góc với mặt phẳng, góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
1.2. Ký Hiệu Góc Giữa Đường Thẳng và Mặt Phẳng
- Nếu đường thẳng (alpha) vuông góc với mặt phẳng (P), ký hiệu là (widehat{(alpha, (P))} = 90^circ).
- Nếu đường thẳng (alpha) không vuông góc với mặt phẳng (P), ký hiệu (widehat{(alpha, (P))} = widehat{(alpha, alpha’)}), trong đó (alpha’) là hình chiếu của (alpha) trên (P).
Lưu ý quan trọng: Góc giữa đường thẳng và mặt phẳng luôn nằm trong khoảng từ 0 độ đến 90 độ: (0^circ leq widehat{(alpha, (P))} leq 90^circ).
2. Các Phương Pháp Xác Định Góc Giữa Đường Thẳng và Mặt Phẳng
Có hai phương pháp chính để xác định góc giữa đường thẳng và mặt phẳng: phương pháp sử dụng vectơ và phương pháp hình học.
2.1. Phương Pháp Vectơ để Tính Góc Giữa Đường Thẳng và Mặt Phẳng
Phương pháp này dựa trên việc sử dụng tích vô hướng của vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng.
-
Bước 1: Xác định vectơ chỉ phương (vec{u} = (a, b, c)) của đường thẳng (d).
-
Bước 2: Xác định vectơ pháp tuyến (vec{n} = (A, B, C)) của mặt phẳng (P).
-
Bước 3: Sử dụng công thức:
[
sin alpha = sin widehat{(d, (P))} = frac{|vec{u} cdot vec{n}|}{|vec{u}| cdot |vec{n}|} = frac{|aA + bB + cC|}{sqrt{a^2 + b^2 + c^2} cdot sqrt{A^2 + B^2 + C^2}}
]
Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a√2. Tính góc giữa SC và mặt phẳng (ABCD).
Giải: Vì SA vuông góc với (ABCD) nên AC là hình chiếu của SC trên (ABCD). Do đó góc giữa SC và (ABCD) là góc SCA.
Ta có: (AC = asqrt{2}). Xét tam giác SAC vuông tại A:
(tan(widehat{SCA}) = frac{SA}{AC} = frac{asqrt{2}}{asqrt{2}} = 1). Vậy (widehat{SCA} = 45^circ).
2.2. Phương Pháp Hình Học để Xác Định Góc Giữa Đường Thẳng và Mặt Phẳng
Phương pháp này tập trung vào việc tìm hình chiếu của đường thẳng lên mặt phẳng.
- Bước 1: Tìm giao điểm (I) của đường thẳng (d) và mặt phẳng (P): (I = d cap (P)).
- Bước 2: Chọn một điểm (A) trên đường thẳng (d) (khác (I)), kẻ đường thẳng (AH) vuông góc với mặt phẳng (P) tại (H).
- Bước 3: Góc giữa đường thẳng (d) và mặt phẳng (P) là góc (widehat{AIH}).
Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = a√3. SA vuông góc với (ABC) và SA = a. Tính góc giữa SC và (ABC).
Giải: Vì SA vuông góc với (ABC), AC là hình chiếu của SC trên (ABC). Do đó góc giữa SC và (ABC) là góc SCA.
Ta có: (AC = sqrt{AB^2 + BC^2} = sqrt{a^2 + 3a^2} = 2a). Xét tam giác SAC vuông tại A:
(tan(widehat{SCA}) = frac{SA}{AC} = frac{a}{2a} = frac{1}{2}). Vậy (widehat{SCA} = arctan(frac{1}{2})).
3. Bài Tập Trắc Nghiệm Minh Họa về Góc Giữa Đường Thẳng và Mặt Phẳng
Dưới đây là một số bài tập trắc nghiệm minh họa, giúp bạn luyện tập và củng cố kiến thức về góc giữa đường thẳng và mặt phẳng.
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với (ABCD) và SA = a. Góc giữa SC và (ABCD) là:
A. 30° B. 45° C. 60° D. 90°
Câu 2. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Góc giữa AC’ và (ABCD) là:
A. 30° B. 45° C. 60° D. 90°
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với (ABC) và SA = a√3. Góc giữa SB và (ABC) là:
A. 30° B. 45° C. 60° D. 90°
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, SA vuông góc với (ABCD) và SA = a. Góc giữa SC và (ABCD) là:
A. 30° B. 45° C. 60° D. arctan(√5/5)
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc BAD = 60°, SA vuông góc với (ABCD) và SA = a. Góc giữa SC và (ABCD) là:
A. 30° B. 45° C. 60° D. 90°
Đáp án:
- B
- B
- C
- D
- B
Qua bài viết này, hy vọng bạn đã nắm vững lý thuyết và Phương Pháp Tính Góc Giữa đường Thẳng Và Mặt Phẳng. Hãy luyện tập thêm các bài tập khác để thành thạo kỹ năng này, giúp bạn tự tin giải quyết các bài toán hình học không gian phức tạp.