Trong hình học, việc xác định một hình có tâm đối xứng hay không là một khái niệm quan trọng. Bài viết này sẽ tập trung vào các Hình Không Có Tâm đối Xứng, cung cấp định nghĩa, ví dụ minh họa và các lưu ý quan trọng để nhận biết chúng một cách dễ dàng.
1. Định nghĩa hình có tâm đối xứng và hình không có tâm đối xứng
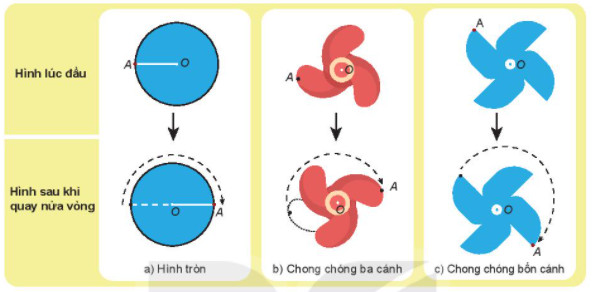
Một hình được gọi là có tâm đối xứng nếu tồn tại một điểm O sao cho khi quay hình đó nửa vòng (180 độ) quanh điểm O, hình mới thu được trùng khớp hoàn toàn với hình ban đầu. Điểm O được gọi là tâm đối xứng của hình.
Ngược lại, nếu không tồn tại điểm O nào thỏa mãn điều kiện trên, hình đó được gọi là hình không có tâm đối xứng.
2. Ví dụ về hình không có tâm đối xứng
Rất nhiều hình quen thuộc trong cuộc sống hàng ngày và trong toán học là hình không có tâm đối xứng. Dưới đây là một vài ví dụ điển hình:
- Tam giác đều: Mặc dù tam giác đều có trục đối xứng, nhưng nó không có tâm đối xứng. Khi quay tam giác đều 180 độ quanh bất kỳ điểm nào, hình mới sẽ không trùng khớp với hình ban đầu.
- Chong chóng ba cánh: Tương tự như ví dụ trong bài gốc, chong chóng ba cánh là một ví dụ trực quan về hình không có tâm đối xứng.
Alt text: Hình ảnh chong chóng ba cánh, minh họa cho một ví dụ điển hình về hình không có tâm đối xứng trong toán học.
- Hình thang cân: Mặc dù hình thang cân có một trục đối xứng, nhưng nó không có tâm đối xứng.
- Các chữ cái: Nhiều chữ cái trong bảng chữ cái tiếng Việt và tiếng Anh không có tâm đối xứng, ví dụ như chữ “P”, “Q”, “F”, “G”, “J”, “L”, “N”, “R”, “S”, “Z”…
3. Cách nhận biết hình không có tâm đối xứng
Để xác định một hình có phải là hình không có tâm đối xứng hay không, ta có thể thực hiện các bước sau:
- Tìm kiếm điểm nghi ngờ: Thử chọn một điểm bất kỳ trên hình.
- Tưởng tượng phép quay: Hình dung việc quay hình đó 180 độ quanh điểm đã chọn.
- So sánh: Kiểm tra xem hình mới thu được có trùng khớp hoàn toàn với hình ban đầu hay không.
- Kết luận: Nếu không tìm được điểm nào thỏa mãn, kết luận hình đó là hình không có tâm đối xứng.
4. Lưu ý quan trọng
- Một hình có trục đối xứng không nhất thiết phải có tâm đối xứng. Ví dụ, hình thang cân có trục đối xứng nhưng không có tâm đối xứng.
- Một hình có tâm đối xứng có thể có hoặc không có trục đối xứng. Ví dụ, hình tròn có tâm đối xứng và vô số trục đối xứng.
5. Ứng dụng của khái niệm hình không có tâm đối xứng
Khái niệm hình không có tâm đối xứng không chỉ quan trọng trong hình học mà còn có ứng dụng trong nhiều lĩnh vực khác, như:
- Thiết kế: Trong thiết kế đồ họa và kiến trúc, việc hiểu rõ tính đối xứng của các hình ảnh và cấu trúc giúp tạo ra những sản phẩm hài hòa và cân đối. Việc sử dụng các hình không có tâm đối xứng có thể tạo ra sự độc đáo và phá cách.
- Nghệ thuật: Các nghệ sĩ thường sử dụng các hình dạng và bố cục đối xứng hoặc bất đối xứng để truyền tải những thông điệp và cảm xúc khác nhau.
Alt text: Sơ đồ tư duy minh họa các loại hình và thuộc tính đối xứng, nhấn mạnh sự khác biệt giữa hình có và không có tâm đối xứng.
Hiểu rõ về hình không có tâm đối xứng giúp chúng ta có cái nhìn sâu sắc hơn về thế giới hình học và ứng dụng nó vào thực tế. Hy vọng bài viết này đã cung cấp những thông tin hữu ích và dễ hiểu về chủ đề này.