Trong hình học không gian, khối trụ tròn xoay là một hình khối quan trọng với nhiều ứng dụng thực tế. Bài viết này sẽ cung cấp một cái nhìn toàn diện về Công Thức Thể Tích Khối Trụ Tròn Xoay, các dạng bài tập liên quan và phương pháp giải quyết chúng một cách hiệu quả, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán.
Khối Trụ Tròn Xoay Là Gì?
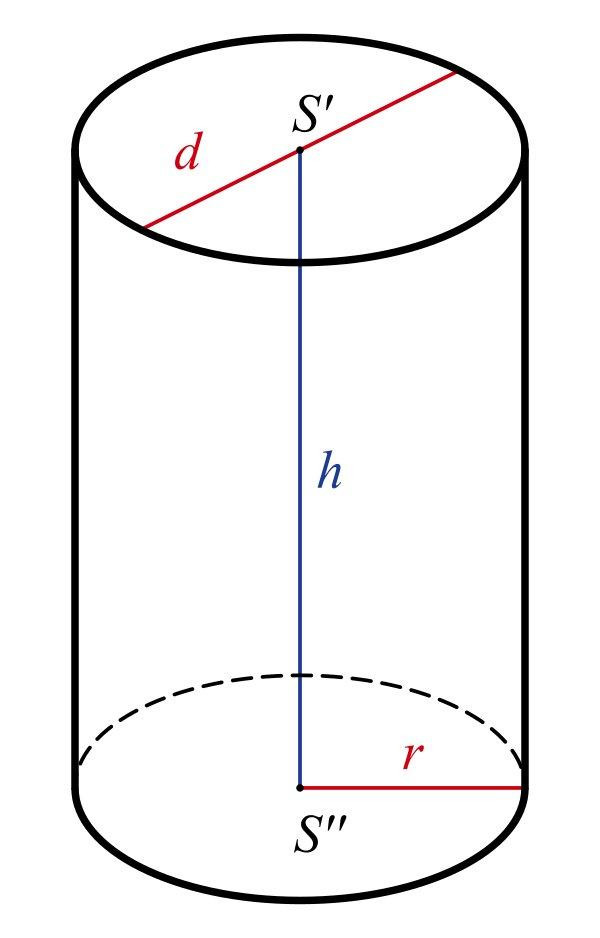
Khối trụ tròn xoay được tạo thành khi quay một hình chữ nhật quanh một trong các cạnh của nó. Trục quay này đóng vai trò là trục đối xứng của khối trụ.
Về cơ bản, khối trụ bao gồm hai đáy là hai hình tròn bằng nhau và một mặt xung quanh là một hình chữ nhật được uốn cong. Thể tích khối trụ tròn xoay là không gian mà khối trụ chiếm giữ.
Công Thức Tính Thể Tích Khối Trụ Tròn Xoay
Công thức tính thể tích khối trụ tròn xoay vô cùng đơn giản và dễ nhớ:
V = πr²h
Trong đó:
- V: Thể tích của khối trụ
- π (pi): Hằng số toán học, xấp xỉ bằng 3.14159
- r: Bán kính của đáy hình tròn
- h: Chiều cao của khối trụ (khoảng cách giữa hai đáy)
Công thức toán học V = πr²h, biểu thị thể tích khối trụ bằng tích của số pi, bình phương bán kính đáy và chiều cao trụ.
Công thức này cho thấy thể tích khối trụ tròn xoay tỉ lệ thuận với bình phương bán kính đáy và chiều cao. Điều này có nghĩa là, nếu tăng bán kính đáy lên gấp đôi, thể tích sẽ tăng lên gấp bốn lần, trong khi tăng chiều cao lên gấp đôi sẽ làm thể tích tăng lên gấp đôi.
Các Dạng Bài Tập Về Thể Tích Khối Trụ Tròn Xoay và Phương Pháp Giải
Các bài tập về công thức thể tích khối trụ tròn xoay thường xoay quanh việc tìm một trong ba yếu tố: thể tích, bán kính đáy hoặc chiều cao, khi biết hai yếu tố còn lại. Dưới đây là một số dạng bài tập thường gặp:
Dạng 1: Tính Thể Tích Khối Trụ Khi Biết Bán Kính Đáy và Chiều Cao
Đây là dạng bài tập cơ bản nhất. Bạn chỉ cần áp dụng trực tiếp công thức thể tích khối trụ tròn xoay để tìm kết quả.
Ví dụ: Một khối trụ có bán kính đáy là 5cm và chiều cao là 10cm. Tính thể tích của khối trụ đó.
Giải:
V = πr²h = π(5cm)²(10cm) ≈ 785.4 cm³
Dạng 2: Tìm Bán Kính Đáy Khi Biết Thể Tích và Chiều Cao
Trong trường hợp này, bạn cần biến đổi công thức thể tích khối trụ tròn xoay để tìm bán kính đáy:
r = √(V / (πh))
Ví dụ: Một khối trụ có thể tích là 314 cm³ và chiều cao là 4cm. Tính bán kính đáy của khối trụ đó.
Giải:
r = √(V / (πh)) = √(314 cm³ / (π * 4cm)) ≈ 5 cm
Dạng 3: Tìm Chiều Cao Khi Biết Thể Tích và Bán Kính Đáy
Tương tự như trên, bạn cần biến đổi công thức thể tích khối trụ tròn xoay để tìm chiều cao:
h = V / (πr²)
Ví dụ: Một khối trụ có thể tích là 628 cm³ và bán kính đáy là 5cm. Tính chiều cao của khối trụ đó.
Giải:
h = V / (πr²) = 628 cm³ / (π * (5cm)²) ≈ 8 cm
Dạng 4: Bài Toán Ứng Dụng Thực Tế
Các bài toán thực tế có thể liên quan đến việc tính thể tích của các vật dụng hình trụ, chẳng hạn như bồn chứa nước, ống nước hoặc các bộ phận máy móc. Điều quan trọng là phải xác định được bán kính đáy và chiều cao từ thông tin đã cho.
Ví dụ: Một bồn chứa nước hình trụ có đường kính đáy là 2 mét và chiều cao là 3 mét. Hỏi bồn chứa này có thể chứa được bao nhiêu mét khối nước?
Giải:
Bán kính đáy: r = đường kính / 2 = 2 mét / 2 = 1 mét
Thể tích: V = πr²h = π(1 mét)²(3 mét) ≈ 9.42 mét khối
Bài Tập Nâng Cao Về Thể Tích Khối Trụ Tròn Xoay
Để nâng cao kỹ năng giải toán, bạn có thể thử sức với các bài tập phức tạp hơn, chẳng hạn như:
- Bài tập kết hợp nhiều hình khối: Tính thể tích của một vật thể được tạo thành từ nhiều khối trụ và các hình khối khác.
- Bài tập liên quan đến diện tích xung quanh và diện tích toàn phần của khối trụ: Sử dụng các công thức diện tích để tìm ra bán kính đáy hoặc chiều cao, sau đó tính thể tích.
- Bài tập có yếu tố biến thiên: Tính thể tích của khối trụ khi bán kính đáy hoặc chiều cao thay đổi theo một quy luật nào đó.
Kết Luận
Nắm vững công thức thể tích khối trụ tròn xoay và các dạng bài tập liên quan là rất quan trọng trong chương trình toán học phổ thông và có nhiều ứng dụng trong thực tế. Bằng cách luyện tập thường xuyên và áp dụng các phương pháp giải toán phù hợp, bạn sẽ có thể tự tin giải quyết mọi bài toán về khối trụ tròn xoay.