Cho tam giác ABC, kẻ AH vuông góc với BC tại H là một cấu hình hình học quen thuộc và cơ bản. Từ cấu hình này, chúng ta có thể phát triển nhiều bài toán thú vị và bổ ích. Dưới đây là một số khía cạnh quan trọng liên quan đến chủ đề này.
Các Tính Chất Cơ Bản
Khi AH vuông góc với BC, ta có các tính chất quan trọng sau:
- AH là đường cao của tam giác ABC.
- Tam giác AHB và AHC là các tam giác vuông.
- Định lý Pythagoras có thể được áp dụng cho các tam giác vuông AHB và AHC.
Ứng Dụng Định Lý Pythagoras
Định lý Pythagoras cho phép chúng ta thiết lập các mối quan hệ về độ dài giữa các cạnh của tam giác vuông. Trong tam giác ABC với AH vuông góc BC, ta có:
- Trong tam giác AHB: $AB^2 = AH^2 + BH^2$
- Trong tam giác AHC: $AC^2 = AH^2 + CH^2$
Từ đó, ta có thể suy ra các công thức và mối liên hệ khác, phục vụ cho việc giải toán.
Ví dụ minh họa: Hình ảnh minh họa tam giác ABC có đường cao AH, giúp học sinh hình dung rõ hơn về các yếu tố và quan hệ trong bài toán.
So Sánh Độ Dài Các Đường
Trong hình học, khi so sánh độ dài các đường, chúng ta cần nhớ một số quy tắc quan trọng:
- Đường vuông góc là đường ngắn nhất nối từ một điểm đến một đường thẳng.
- Đường xiên luôn dài hơn đường vuông góc.
Ví dụ, nếu xét điểm A và đường thẳng BC, thì AH (đường vuông góc) sẽ ngắn hơn bất kỳ đường xiên nào khác kẻ từ A đến BC.
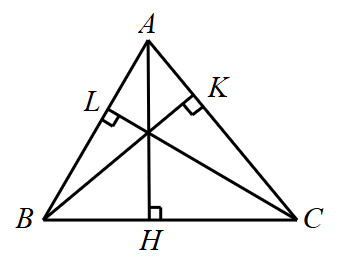Hình ảnh minh họa AH là đường vuông góc ngắn nhất từ A đến BC, BK là đường xiên
Ví dụ minh họa: AH là đường vuông góc, AK là đường xiên từ A đến BC.
Bài Toán Chứng Minh Bất Đẳng Thức
Với cấu hình “Cho Tam Giác Abc Kẻ Ah Vuông Góc Với Bc,” chúng ta có thể xây dựng các bài toán chứng minh bất đẳng thức liên quan đến độ dài các đoạn thẳng.
Ví dụ: Chứng minh rằng nếu AB < AC thì BH < CH.
Hướng dẫn giải:
- Áp dụng định lý Pythagoras cho tam giác AHB và AHC.
- Sử dụng giả thiết AB < AC để suy ra mối quan hệ giữa BH và CH.
Ví dụ minh họa: So sánh BH và CH khi AB < AC.
Tính Diện Tích Tam Giác
Đường cao AH đóng vai trò quan trọng trong việc tính diện tích tam giác ABC. Công thức tính diện tích tam giác là:
$S = frac{1}{2} cdot BC cdot AH$
Trong đó:
- S là diện tích tam giác ABC.
- BC là độ dài cạnh đáy.
- AH là độ dài đường cao tương ứng với cạnh đáy BC.
Các Bài Toán Nâng Cao
Từ cấu hình cơ bản, ta có thể phát triển các bài toán phức tạp hơn, kết hợp với các kiến thức khác như:
- Đường trung tuyến
- Đường phân giác
- Đường tròn nội tiếp, ngoại tiếp
Những bài toán này đòi hỏi sự linh hoạt trong việc áp dụng các định lý và tính chất hình học.
Kết Luận
Việc “cho tam giác ABC kẻ AH vuông góc với BC” là một chủ đề quan trọng trong hình học, mở ra nhiều bài toán và ứng dụng thú vị. Hiểu rõ các tính chất và định lý liên quan sẽ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả. Việc luyện tập thường xuyên với các dạng bài tập khác nhau sẽ củng cố kiến thức và kỹ năng giải toán.
