Công thức (x+y+z)^2 là một biểu thức đại số cơ bản, nhưng nó lại có những ứng dụng quan trọng trong nhiều lĩnh vực, đặc biệt là trong lĩnh vực lượng tử, liên quan đến việc mã hóa và sửa lỗi lượng tử.
Công Thức Tổng Quát
Công thức khai triển của (x+y+z)^2 là:
(x + y + z)^2 = x^2 + y^2 + z^2 + 2xy + 2yz + 2zx
Công thức này cho thấy bình phương của tổng ba số bằng tổng bình phương của từng số cộng với hai lần tích của từng cặp số.
Ứng Dụng Trong Mã Sửa Lỗi Lượng Tử
Trong lĩnh vực máy tính lượng tử, việc bảo vệ thông tin lượng tử (qubit) khỏi các lỗi là vô cùng quan trọng. Một trong những phương pháp để đạt được điều này là sử dụng mã sửa lỗi lượng tử. Một ví dụ điển hình là mã ổn định tử XYZ², lấy cảm hứng từ mô hình Kitaev.
Mã XYZ² được xây dựng trên một lưới lục giác tổ ong, sử dụng các phép đo ổn định để phát hiện và sửa lỗi. Mã này có các tính chất đặc biệt, bao gồm khả năng chống lại các loại lỗi khác nhau với các ngưỡng lỗi khác nhau.
Mã XYZ² và các tính chất
Mã XYZ² sử dụng các qubit được sắp xếp trên lưới lục giác. Các stabilizer (toán tử ổn định) được định nghĩa như sau:
- Ổn định tử mặt (Plaquette stabilizers): Trọng số sáu (XYZXYZ)
- Ổn định tử cạnh (Link stabilizers): Trọng số hai (XX)
- Ổn định tử biên (Boundary stabilizers): Trọng số ba
Mục đích của việc sử dụng các stabilizer này là tạo ra một không gian mã hóa, trong đó thông tin lượng tử được lưu trữ một cách an toàn. Khi có lỗi xảy ra, các stabilizer sẽ phát hiện ra sự thay đổi trong trạng thái của các qubit và cung cấp thông tin để sửa lỗi.
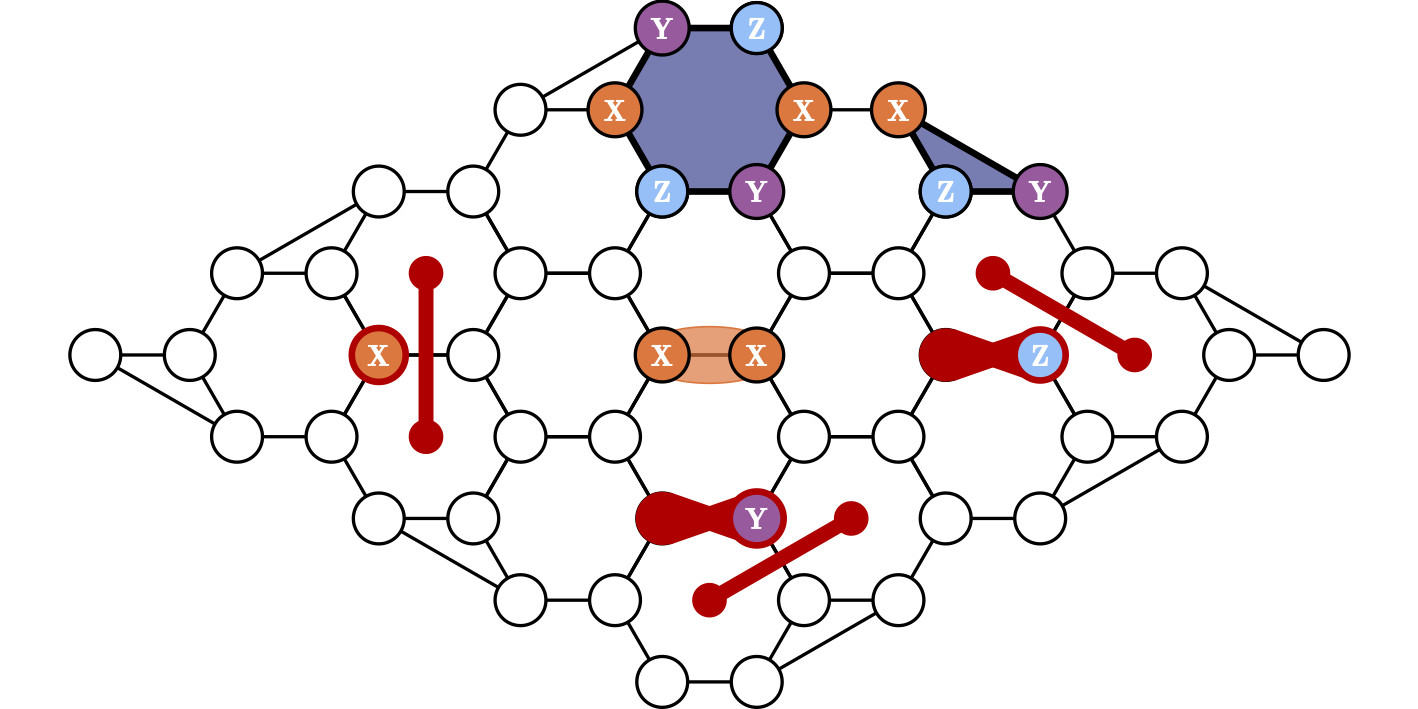
Ảnh mô tả cấu trúc mã XYZ² khoảng cách 5, cùng các stabilizer cạnh, mặt và biên. Các syndrome (hội chứng lỗi) cho các lỗi X, Y và Z riêng lẻ cũng được thể hiện rõ. Mã này có khả năng sửa lỗi lượng tử nhờ cấu trúc đặc biệt của nó.
Ngưỡng Lỗi và Hiệu Suất
Một trong những yếu tố quan trọng nhất của một mã sửa lỗi lượng tử là ngưỡng lỗi của nó. Ngưỡng lỗi là tỷ lệ lỗi vật lý tối đa mà mã có thể sửa mà vẫn đảm bảo tỷ lệ lỗi logic giảm khi tăng kích thước mã.
Mã XYZ² có ngưỡng lỗi cao cho các loại lỗi thiên lệch. Điều này có nghĩa là mã này đặc biệt hiệu quả trong việc sửa các lỗi mà một loại lỗi nào đó (ví dụ: lỗi pha Z) phổ biến hơn các loại lỗi khác (ví dụ: lỗi bit X). Trong trường hợp lỗi X, Y hoặc Z thuần túy, ngưỡng có thể đạt tới 50%.
So sánh với các Mã Sửa Lỗi Lượng Tử Khác
So với mã bề mặt xoay và mã XZZX, mã XYZ² có một số ưu điểm nhất định. Ví dụ, mã XYZ² có khoảng cách mã là 2d² cho cả lỗi Z và lỗi Y thuần túy, trong khi mã bề mặt xoay và mã XZZX chỉ có khoảng cách mã là d² cho lỗi Y thuần túy.
Ứng Dụng Tiềm Năng
Mã XYZ² có nhiều ứng dụng tiềm năng trong lĩnh vực máy tính lượng tử. Nó có thể được sử dụng để xây dựng các máy tính lượng tử chịu lỗi, có khả năng thực hiện các phép tính phức tạp mà không bị ảnh hưởng bởi các lỗi lượng tử.
Kết Luận
Công thức (x+y+z)^2 tưởng chừng đơn giản nhưng lại có vai trò quan trọng trong việc phát triển các mã sửa lỗi lượng tử tiên tiến như mã XYZ². Những mã này đóng vai trò then chốt trong việc hiện thực hóa máy tính lượng tử chịu lỗi, mở ra một kỷ nguyên mới trong lĩnh vực điện toán. Nghiên cứu và phát triển các mã sửa lỗi lượng tử hiệu quả là một trong những ưu tiên hàng đầu trong lĩnh vực máy tính lượng tử hiện nay.
