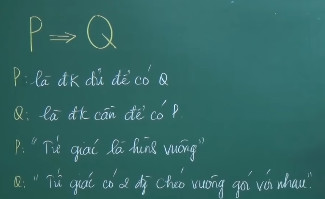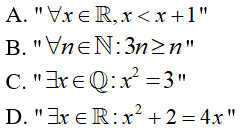Xét Tính Đúng Sai Của Mệnh Đề: Lý Thuyết, Phương Pháp Giải & Bài Tập

donghochetacdh

4 days ago

Mệnh đề và tính đúng sai: Ví dụ minh họa về các loại câu khẳng định, câu hỏi và mệnh đề.

1. Tổng Quan Lý Thuyết Về Mệnh Đề

1.1. Định Nghĩa Mệnh Đề

Mệnh đề là một câu khẳng định có giá trị chân lý xác định, nghĩa là có thể xác định được là đúng hoặc sai. Tính đúng sai của mệnh đề là một thuộc tính quan trọng để phân biệt nó với các loại câu khác.

Ví dụ:

“Hà Nội là thủ đô của Việt Nam” là một mệnh đề đúng.
“2 + 2 = 5” là một mệnh đề sai.
“Bạn có khỏe không?” không phải là một mệnh đề vì nó là một câu hỏi, không phải là một khẳng định.

1.2. Các Dạng Mệnh Đề Thường Gặp

1.2.1. Mệnh Đề Phủ Định

Mệnh đề phủ định của mệnh đề A, ký hiệu là ¬A, là mệnh đề có giá trị chân lý ngược lại với A. Nếu A đúng thì ¬A sai, và ngược lại. Việc xác định mệnh đề phủ định giúp ta hiểu rõ hơn về ý nghĩa của mệnh đề gốc và Xét Tính đúng Sai Của Mệnh đề một cách logic.

Ví dụ:

A: “Hôm nay trời mưa.”
¬A: “Hôm nay trời không mưa.”

1.2.2. Mệnh Đề Kéo Theo (Điều Kiện)

Mệnh đề kéo theo, ký hiệu là A → B, có dạng “Nếu A thì B”. Mệnh đề này chỉ sai khi A đúng và B sai. Trong các trường hợp còn lại, mệnh đề kéo theo luôn đúng. Việc nắm vững quy tắc này rất quan trọng khi xét tính đúng sai của mệnh đề phức tạp.

Ví dụ:

A: “Tam giác ABC là tam giác đều.”
B: “Tam giác ABC có ba cạnh bằng nhau.”
A → B: “Nếu tam giác ABC là tam giác đều thì tam giác ABC có ba cạnh bằng nhau.” (Đúng)

1.2.3. Mệnh Đề Đảo

Mệnh đề đảo của A → B là B → A. Mệnh đề đảo không nhất thiết có cùng giá trị chân lý với mệnh đề gốc. Việc xem xét mệnh đề đảo giúp ta hiểu rõ hơn về tính tương quan giữa các mệnh đề.

Ví dụ:

A → B: “Nếu một tứ giác là hình vuông thì nó là hình chữ nhật.” (Đúng)
B → A: “Nếu một tứ giác là hình chữ nhật thì nó là hình vuông.” (Sai)

1.2.4. Mệnh Đề Tương Đương

Mệnh đề tương đương, ký hiệu là A ↔ B, đúng khi A và B cùng đúng hoặc cùng sai. Mệnh đề tương đương thể hiện mối quan hệ hai chiều và mạnh mẽ giữa hai mệnh đề. Để xét tính đúng sai của mệnh đề tương đương, ta cần chứng minh cả A → B và B → A đều đúng.

Ví dụ:

A: “x là số chẵn.”
B: “x chia hết cho 2.”
A ↔ B: “x là số chẵn khi và chỉ khi x chia hết cho 2.” (Đúng)

1.2.5. Mệnh Đề Chứa Ký Hiệu ∀, ∃ (Lượng Từ)

∀ (với mọi): ∀x ∈ X, P(x) nghĩa là “với mọi x thuộc tập hợp X, mệnh đề P(x) đúng”.
∃ (tồn tại): ∃x ∈ X, P(x) nghĩa là “tồn tại một x thuộc tập hợp X sao cho mệnh đề P(x) đúng”.

Việc xét tính đúng sai của mệnh đề chứa lượng từ đòi hỏi việc kiểm tra tính đúng đắn của mệnh đề P(x) với tất cả hoặc ít nhất một phần tử của tập hợp X.

Ví dụ:

∀x ∈ R, x² ≥ 0 (Đúng)
∃x ∈ R, x² = -1 (Sai)

2. Hướng Dẫn Xét Tính Đúng Sai Của Mệnh Đề và Bài Tập Luyện Tập

2.1. Phương Pháp Giải

Xác định dạng mệnh đề: Xác định xem mệnh đề thuộc dạng nào (đơn, phủ định, kéo theo, tương đương, chứa lượng từ).
Phân tích cấu trúc: Phân tích các thành phần của mệnh đề và mối quan hệ giữa chúng.
Áp dụng quy tắc: Áp dụng các quy tắc về giá trị chân lý của từng dạng mệnh đề để xác định tính đúng sai.
Chứng minh (nếu cần): Đối với mệnh đề phức tạp, cần sử dụng phương pháp chứng minh trực tiếp, phản chứng, hoặc quy nạp để kết luận.

Ví dụ 1: Xét tính đúng sai của mệnh đề: “Nếu 2 là số chẵn thì 3 là số lẻ.”