Bài viết này sẽ cung cấp kiến thức toàn diện về Xét Tam Giác Vuông, bao gồm các trường hợp bằng nhau và ứng dụng giải bài tập, giúp học sinh nắm vững kiến thức và tự tin chinh phục các bài toán hình học.
1. Khái Niệm Tam Giác Bằng Nhau
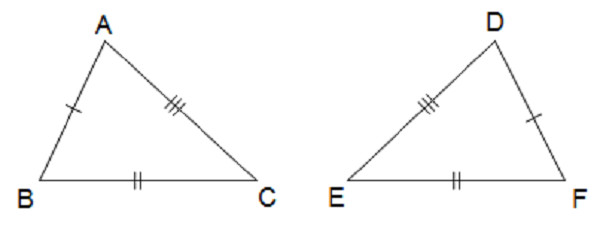
Hai tam giác được gọi là bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.
Hình ảnh minh họa hai tam giác bằng nhau, nhấn mạnh sự tương ứng giữa các cạnh và góc.
2. Các Trường Hợp Bằng Nhau Của Tam Giác Vuông
Tam giác vuông có một góc bằng 90 độ, do đó việc chứng minh hai tam giác vuông bằng nhau trở nên đơn giản hơn so với tam giác thường. Dưới đây là các trường hợp bằng nhau của xét tam giác vuông:
2.1. Hai Cạnh Góc Vuông (c-g-c)
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.
2.2. Cạnh Góc Vuông và Góc Nhọn Kề (g-c-g)
Nếu một cạnh góc vuông và một góc nhọn kề cạnh đó của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh đó của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.
2.3. Cạnh Huyền và Góc Nhọn (g-c-g)
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.
Hình ảnh trực quan về hai tam giác vuông có cạnh huyền và một góc nhọn tương ứng bằng nhau.
2.4. Cạnh Huyền và Cạnh Góc Vuông (c-c-c)
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.
Hình ảnh minh họa trực quan hai tam giác vuông bằng nhau khi có cạnh huyền và một cạnh góc vuông bằng nhau.
3. Các Dạng Bài Tập Thường Gặp Về Xét Tam Giác Vuông
3.1. Chứng Minh Hai Tam Giác Vuông Bằng Nhau
- Phương pháp: Xét hai tam giác vuông, kiểm tra các điều kiện bằng nhau (c-g-c, g-c-g, cạnh huyền – góc nhọn, cạnh huyền – cạnh góc vuông) và kết luận.
3.2. Chứng Minh Góc và Đoạn Thẳng Bằng Nhau
- Phương pháp: Chứng minh hai tam giác vuông chứa các góc hoặc đoạn thẳng cần chứng minh bằng nhau, suy ra các yếu tố tương ứng bằng nhau.
3.3. Tìm Điều Kiện Để Hai Tam Giác Vuông Bằng Nhau
- Phương pháp: Phân tích các yếu tố đã biết của hai tam giác vuông, xác định yếu tố còn thiếu để áp dụng một trong các trường hợp bằng nhau.
4. Ví Dụ Minh Họa
Ví dụ 1: Cho tam giác ABC vuông tại A, có AB = AC. Chứng minh rằng góc B = góc C.
- Giải: Vì AB = AC nên tam giác ABC là tam giác vuông cân tại A. Do đó, góc B = góc C = 45 độ.
Ví dụ 2: Cho hai tam giác vuông ABC và DEF có góc A = góc D = 90 độ, AB = DE, BC = EF. Chứng minh rằng tam giác ABC = tam giác DEF.
-
Giải: Xét hai tam giác vuông ABC và DEF có:
- AB = DE (giả thiết)
- BC = EF (giả thiết)
- Vậy tam giác ABC = tam giác DEF (cạnh huyền – cạnh góc vuông)
5. Bài Tập Luyện Tập
- Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC. Chứng minh rằng tam giác ABH và tam giác CAH đồng dạng.
- Cho tam giác MNP vuông tại M, có MN < MP. Trên cạnh MP lấy điểm E sao cho ME = MN. Chứng minh rằng NE là tia phân giác của góc MNP.
- Cho hình vuông ABCD. Trên cạnh AB lấy điểm E, trên cạnh BC lấy điểm F sao cho AE = BF. Chứng minh rằng tam giác ADE = tam giác BCF.
Hiểu rõ và vận dụng linh hoạt các trường hợp bằng nhau của xét tam giác vuông là chìa khóa để giải quyết các bài toán hình học một cách hiệu quả. Chúc các bạn học tốt!
Hình ảnh hai tam giác bằng nhau, thể hiện khái niệm tổng quan về sự tương đồng hình dạng và kích thước.