Góc Giữa Mặt Bên và Mặt Đáy: Khái Niệm
Góc giữa mặt bên và mặt đáy của một hình chóp hoặc hình lăng trụ là góc tạo bởi một đường thẳng nằm trên mặt bên và vuông góc với giao tuyến của mặt bên và mặt đáy, và một đường thẳng nằm trên mặt đáy và cũng vuông góc với giao tuyến đó. Việc xác định chính xác góc này là một kỹ năng quan trọng trong hình học không gian.
Các Bước Xác Định Góc Giữa Mặt Bên và Mặt Đáy
Để Xác định Góc Giữa Mặt Bên Và Mặt đáy, chúng ta thường thực hiện theo các bước sau:
- Tìm giao tuyến: Xác định giao tuyến của mặt bên và mặt đáy. Đây là đường thẳng chung của hai mặt phẳng.
- Dựng đường vuông góc: Từ một điểm trên giao tuyến, dựng một đường thẳng vuông góc với giao tuyến và nằm trên mặt đáy.
- Dựng đường vuông góc thứ hai: Từ cùng điểm đó, dựng một đường thẳng vuông góc với giao tuyến và nằm trên mặt bên.
- Xác định góc: Góc giữa hai đường thẳng vừa dựng chính là góc giữa mặt bên và mặt đáy.
Hình ảnh minh họa phương pháp dựng đường vuông góc chung để tìm góc giữa mặt bên và mặt đáy, giúp học sinh hình dung rõ ràng các bước thực hiện.
Phương Pháp Xác Định Giao Tuyến
Để tìm giao tuyến giữa hai mặt phẳng, hãy làm theo các bước sau:
- Tìm hai điểm chung: Xác định hai điểm phân biệt thuộc cả hai mặt phẳng.
- Kết nối hai điểm: Đường thẳng đi qua hai điểm này chính là giao tuyến của hai mặt phẳng.
Hình ảnh trực quan minh họa cách xác định giao tuyến của hai mặt phẳng, nhấn mạnh vai trò của việc tìm hai điểm chung.
Tính Góc Giữa Mặt Bên và Mặt Đáy Bằng Hệ Thức Lượng
Trong nhiều trường hợp, việc tính góc giữa mặt bên và mặt đáy có thể được thực hiện bằng cách sử dụng các hệ thức lượng trong tam giác vuông hoặc định lý hàm số sin, cosin.
Ví dụ: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại A, cạnh BC = 2a, cạnh SA vuông góc với mặt phẳng đáy (ABC), SA = a. Xác định và tính số đo góc giữa hai mặt phẳng (SBC) và (ABC).
Hình ảnh này minh họa cách xác định góc giữa mặt phẳng (SBC) và (ABC) trong một hình chóp cụ thể, giúp người đọc dễ dàng hình dung và áp dụng vào các bài toán tương tự.
Sử Dụng Mặt Phẳng Phụ Để Tính Góc
Đôi khi, việc dựng thêm một mặt phẳng phụ có thể giúp đơn giản hóa việc tính góc giữa mặt bên và mặt đáy.
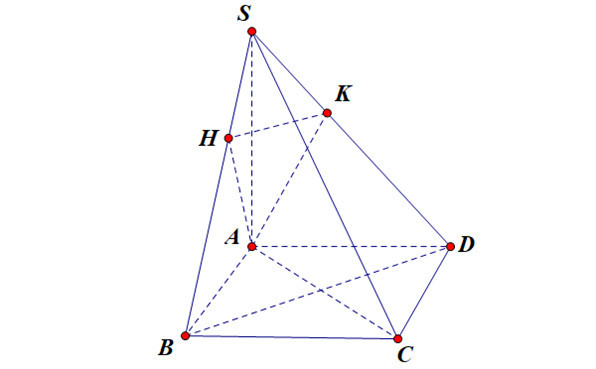
Ví dụ: Cho hình chóp S.ABCD, cạnh đáy ABCD là nửa lục giác đều nội tiếp đường tròn có đường kính AB = 2a, SA vuông góc với mặt phẳng (ABCD) và SA=a√3. Tính góc giữa hai mặt phẳng (SBC) và (SCD).
Hình ảnh này minh họa việc sử dụng mặt phẳng phụ để tính góc giữa (SBC) và (SCD), một kỹ thuật quan trọng trong giải toán hình học không gian.
Bài Tập Vận Dụng
Ví dụ 1: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Tính góc giữa một mặt bên và một mặt đáy.
Hình ảnh minh họa hình chóp tứ giác đều, hỗ trợ việc hình dung và giải bài tập về góc giữa mặt bên và mặt đáy.