Trong chương trình Toán lớp 9, một trong những kỹ năng quan trọng là làm việc với các biểu thức liên quan đến nghiệm của phương trình bậc hai. Đặc biệt, biểu thức $x_1^3 + x_2^3$, trong đó $x_1$ và $x_2$ là nghiệm của phương trình bậc hai, thường xuyên xuất hiện trong các bài toán. Bài viết này sẽ giúp bạn hiểu rõ hơn về cách tính và ứng dụng của biểu thức này.
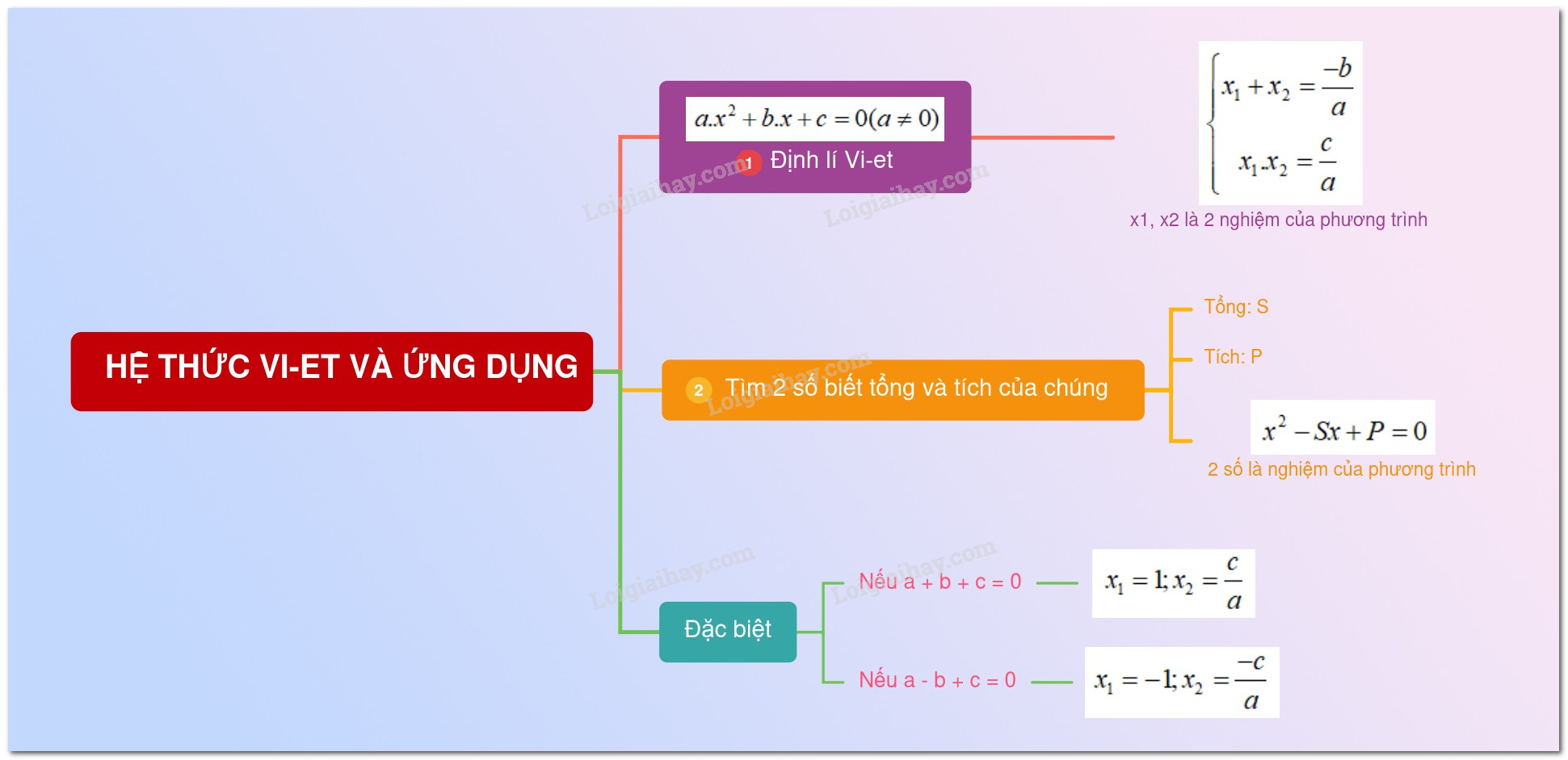
Hệ thức Vi-ét và ứng dụng
Để giải quyết các bài toán liên quan đến $x_1^3 + x_2^3$, chúng ta cần nắm vững hệ thức Vi-ét. Cho phương trình bậc hai $ax^2 + bx + c = 0$ (với $a ne 0$), nếu phương trình có hai nghiệm $x_1$ và $x_2$, thì:
- Tổng hai nghiệm: $x_1 + x_2 = -dfrac{b}{a}$
- Tích hai nghiệm: $x_1 cdot x_2 = dfrac{c}{a}$
Hệ thức Vi-ét là công cụ quan trọng để liên hệ giữa các nghiệm và các hệ số của phương trình bậc hai.
Hình ảnh minh họa hệ thức Vi-ét và ứng dụng trong giải toán lớp 9, giúp học sinh dễ dàng hình dung và ghi nhớ công thức.
Tính $x_1^3 + x_2^3$
Để tính $x_1^3 + x_2^3$, ta có thể sử dụng hằng đẳng thức sau:
$x_1^3 + x_2^3 = (x_1 + x_2)^3 – 3x_1x_2(x_1 + x_2)$
Sử dụng hệ thức Vi-ét, ta có thể thay thế $(x_1 + x_2)$ và $(x_1x_2)$ bằng các hệ số của phương trình bậc hai:
$x_1^3 + x_2^3 = left(-dfrac{b}{a}right)^3 – 3left(dfrac{c}{a}right)left(-dfrac{b}{a}right) = -dfrac{b^3}{a^3} + dfrac{3bc}{a^2}$
Ví dụ minh họa
Xét phương trình $x^2 – 5x + 6 = 0$. Ta có $a = 1, b = -5, c = 6$. Theo hệ thức Vi-ét:
- $x_1 + x_2 = -dfrac{-5}{1} = 5$
- $x_1 cdot x_2 = dfrac{6}{1} = 6$
Vậy, $x_1^3 + x_2^3 = (5)^3 – 3(6)(5) = 125 – 90 = 35$.
Ứng dụng của $x_1^3 + x_2^3$
Biểu thức $x_1^3 + x_2^3$ thường xuất hiện trong các bài toán yêu cầu tìm giá trị của một biểu thức liên quan đến nghiệm của phương trình bậc hai. Nó cũng có thể được sử dụng để xác định điều kiện của tham số để phương trình có nghiệm thỏa mãn một tính chất nào đó.
Ví dụ, xét bài toán sau: Cho phương trình $x^2 – 2mx + m^2 – 1 = 0$. Tìm $m$ để $x_1^3 + x_2^3 = 8$.
Ta có:
- $x_1 + x_2 = 2m$
- $x_1 cdot x_2 = m^2 – 1$
$x_1^3 + x_2^3 = (2m)^3 – 3(m^2 – 1)(2m) = 8m^3 – 6m^3 + 6m = 2m^3 + 6m$
Theo đề bài, $2m^3 + 6m = 8 Rightarrow m^3 + 3m – 4 = 0 Rightarrow (m – 1)(m^2 + m + 4) = 0$.
Vì $m^2 + m + 4 > 0$ với mọi $m$, nên $m = 1$.
Các dạng toán thường gặp và phương pháp giải
- Dạng 1: Tính giá trị biểu thức liên quan đến nghiệm khi biết phương trình.
- Dạng 2: Tìm điều kiện của tham số để biểu thức liên quan đến nghiệm thỏa mãn một điều kiện cho trước.
- Dạng 3: Giải phương trình bằng cách nhẩm nghiệm và sử dụng hệ thức Vi-ét.
 Bài tập về hệ thức Vi-ét
Bài tập về hệ thức Vi-ét
Hình ảnh minh họa một bài tập điển hình về hệ thức Vi-ét, giúp học sinh ôn luyện và nắm vững kiến thức.
Bài tập vận dụng
Bài 1: Cho phương trình $2x^2 – 3x + 1 = 0$. Tính $x_1^3 + x_2^3$.
Bài 2: Cho phương trình $x^2 – 2(m + 1)x + m^2 + 2 = 0$. Tìm $m$ để $x_1^3 + x_2^3 = 20$.
Bài 3: Cho phương trình $x^2 – 4x + m = 0$. Tìm $m$ để $x_1^3 + x_2^3$ đạt giá trị nhỏ nhất.
Hiểu rõ về cách tính và ứng dụng của $x_1^3 + x_2^3$ sẽ giúp bạn tự tin hơn khi giải các bài toán liên quan đến phương trình bậc hai trong chương trình Toán lớp 9. Chúc các bạn học tốt!
