Vòng Tròn Sin Cos, hay còn gọi là vòng tròn lượng giác, là một công cụ toán học mạnh mẽ giúp đơn giản hóa việc hiểu và tính toán các hàm số lượng giác. Từ việc giải các bài toán hình học đến ứng dụng trong vật lý, vòng tròn lượng giác đóng vai trò không thể thiếu. Bài viết này sẽ cung cấp một cái nhìn toàn diện về vòng tròn sin cos, bao gồm định nghĩa, cách sử dụng, các giá trị lượng giác quan trọng, công thức liên kết và các ứng dụng thực tế.
Vòng Tròn Lượng Giác Là Gì?
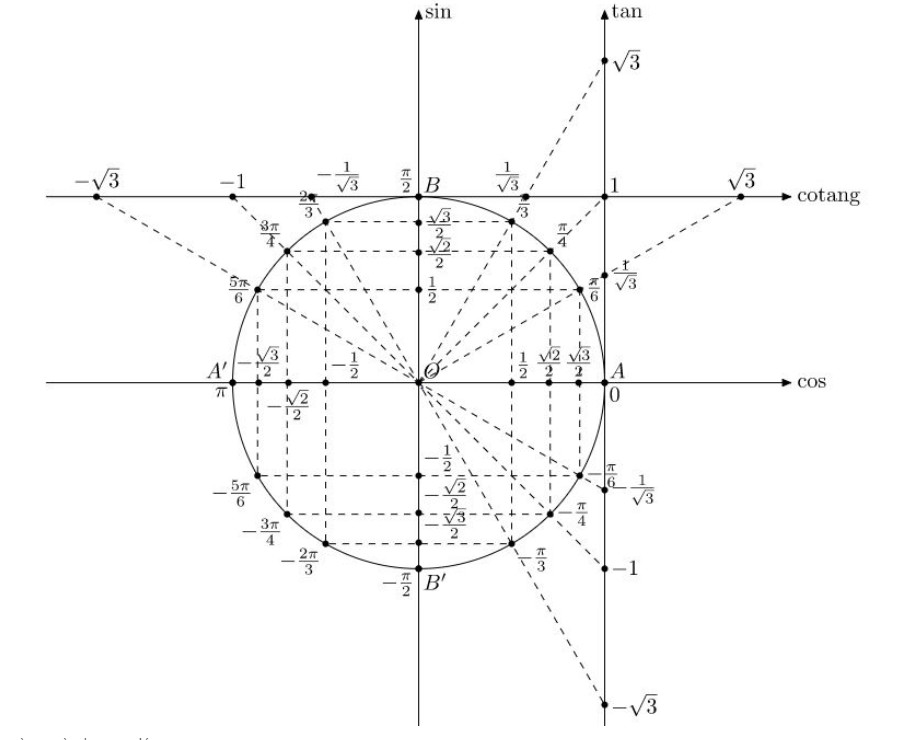
Vòng tròn lượng giác là một đường tròn có bán kính bằng 1, tâm đặt tại gốc tọa độ của hệ trục tọa độ Oxy. Trên vòng tròn này, các góc được đo theo chiều ngược chiều kim đồng hồ, bắt đầu từ trục Ox dương. Mỗi điểm trên vòng tròn tương ứng với một góc, và tọa độ của điểm đó biểu diễn giá trị cosin và sin của góc đó.
Vòng tròn lượng giác đơn giản hóa việc biểu diễn và tính toán các giá trị lượng giác. Điểm P(x, y) trên đường tròn lượng giác tương ứng với góc α, trong đó x = cos(α) và y = sin(α).
Cách Sử Dụng Vòng Tròn Sin Cos
Để sử dụng vòng tròn sin cos hiệu quả, cần nắm vững các yếu tố sau:
- Đường tròn đơn vị: Vòng tròn có bán kính bằng 1, tâm tại gốc tọa độ.
- Chiều dương: Chiều ngược chiều kim đồng hồ là chiều dương để đo góc.
- Trục cos và trục sin: Trục Ox là trục cosin, trục Oy là trục sin.
- Điểm gốc: Điểm A nằm trên trục Ox dương là điểm gốc (góc 0 độ).
Vòng tròn lượng giác cho phép xác định trực quan giá trị sin và cos của một góc bất kỳ. Góc α được tạo bởi tia OA và tia OP, với P là một điểm trên vòng tròn. Hoành độ của P là cos(α) và tung độ của P là sin(α).
Dấu Của Các Giá Trị Lượng Giác
Dấu của các giá trị sin, cos, tan, cot phụ thuộc vào góc phần tư mà góc đó thuộc về:
- Góc phần tư I: Sin (+), Cos (+), Tan (+), Cot (+)
- Góc phần tư II: Sin (+), Cos (-), Tan (-), Cot (-)
- Góc phần tư III: Sin (-), Cos (-), Tan (+), Cot (+)
- Góc phần tư IV: Sin (-), Cos (+), Tan (-), Cot (-)
| Góc phần tư số | I | II | III | IV |
|---|---|---|---|---|
| Giá trị lượng giác | ||||
| sin x | + | + | – | – |
| cos x | + | – | – | + |
| tan x | + | – | + | – |
| cot x | + | – | + | – |

Hiểu rõ quy tắc dấu giúp xác định nhanh chóng giá trị âm dương của các hàm số lượng giác.
Bảng Giá Trị Lượng Giác Đặc Biệt
Bảng giá trị lượng giác của các góc đặc biệt (0°, 30°, 45°, 60°, 90°, 180°) là kiến thức nền tảng:
| α (độ) | 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
|---|---|---|---|---|---|---|---|---|
| α (radian) | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin α | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 |
| cos α | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
| tan α | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot α | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
Công Thức Lượng Giác Liên Kết
Các công thức lượng giác liên kết giúp chuyển đổi giữa các giá trị lượng giác của các góc có mối quan hệ đặc biệt:
- Góc đối nhau: cos(-α) = cos(α); sin(-α) = -sin(α)
- Góc bù nhau: sin(π – α) = sin(α); cos(π – α) = -cos(α)
- Góc phụ nhau: sin(π/2 – α) = cos(α); cos(π/2 – α) = sin(α)
- Góc hơn kém π: tan(π + α) = tan(α); cot(π + α) = cot(α)
Ứng Dụng Của Vòng Tròn Sin Cos
Vòng tròn sin cos có nhiều ứng dụng quan trọng trong toán học và vật lý:
- Toán học: Giải phương trình lượng giác, chứng minh đẳng thức lượng giác, biểu diễn số phức.
- Vật lý: Mô tả dao động điều hòa, phân tích chuyển động tròn, nghiên cứu sóng cơ học và sóng điện từ.
Ví dụ, trong dao động điều hòa, vị trí của vật có thể được biểu diễn bằng phương trình x = Acos(ωt + φ), trong đó A là biên độ, ω là tần số góc, t là thời gian và φ là pha ban đầu. Vòng tròn lượng giác giúp hình dung và tính toán các đại lượng này.
Bài Tập Vận Dụng
Câu 1: Cho góc α thỏa mãn π < α < 3π/2. Xác định dấu của cos(α) và sin(α).
Đáp án: cos(α) < 0, sin(α) < 0 (vì α thuộc góc phần tư thứ III)
Câu 2: Tìm giá trị của sin(210°).
Đáp án: sin(210°) = sin(180° + 30°) = -sin(30°) = -1/2
Câu 3: Giải phương trình cos(x) = √3/2.
Đáp án: x = ±π/6 + k2π, với k là số nguyên.
Vòng tròn sin cos là công cụ vô giá trong việc học và ứng dụng lượng giác. Việc nắm vững các kiến thức cơ bản và luyện tập thường xuyên sẽ giúp bạn sử dụng vòng tròn lượng giác một cách thành thạo và hiệu quả.