Hình Chóp Đều Đáy Vuông: Tất Tần Tật Kiến Thức và Bài Tập

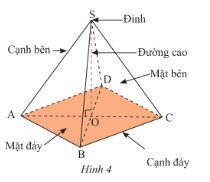
I. Định Nghĩa và Đặc Điểm của Hình Chóp Đều Có Đáy Là Hình Vuông

Hình chóp đều có đáy là hình vuông là một hình chóp đặc biệt, sở hữu những tính chất hình học quan trọng và được ứng dụng rộng rãi trong nhiều bài toán. Để hiểu rõ, ta cần nắm vững định nghĩa và các đặc điểm của nó.

Định nghĩa: Hình chóp đều có đáy là hình vuông là hình chóp có đáy là hình vuông và các cạnh bên bằng nhau.

Các đặc điểm quan trọng:

• Đáy: Là hình vuông.
• Các cạnh bên: Bằng nhau.
• Mặt bên: Là các tam giác cân bằng nhau, có chung một đỉnh (đỉnh của hình chóp).
• Chân đường cao: Trùng với giao điểm của hai đường chéo của hình vuông đáy (tâm của hình vuông). Điều này có nghĩa là đường cao của hình chóp hạ từ đỉnh vuông góc với đáy tại tâm của hình vuông.

Alt text: Mô tả hình chóp tứ giác đều có đáy là hình vuông ABCD và đỉnh S, đường cao SO vuông góc với đáy tại O.

II. Công Thức Tính Diện Tích và Thể Tích

1. Diện Tích Xung Quanh

Diện tích xung quanh của hình chóp đều có đáy là hình vuông là tổng diện tích của bốn mặt bên. Do các mặt bên là các tam giác cân bằng nhau, ta có công thức:

Sxq = p * d

Trong đó:

• Sxq: Diện tích xung quanh.
• p: Nửa chu vi đáy (nửa chu vi hình vuông). Nếu cạnh hình vuông là a, thì p = 2a.
• d: Độ dài trung đoạn (chiều cao của một mặt bên, kẻ từ đỉnh hình chóp xuống cạnh đáy của mặt bên đó).

Alt text: Hình ảnh minh họa công thức tính diện tích xung quanh của hình chóp đều: Sxq = p.d, trong đó p là nửa chu vi đáy và d là trung đoạn.

2. Thể Tích

Thể tích của hình chóp đều có đáy là hình vuông được tính bằng công thức:

V = (1/3) * Sđáy * h

Trong đó:

• V: Thể tích.
• Sđáy: Diện tích đáy (diện tích hình vuông). Nếu cạnh hình vuông là a, thì Sđáy = a^2.
• h: Chiều cao của hình chóp (khoảng cách từ đỉnh đến mặt đáy).

Alt text: Hình ảnh minh họa công thức tính thể tích hình chóp đều: V = (1/3) Sđáy h, trong đó Sđáy là diện tích đáy và h là chiều cao.

Ví dụ:

Cho hình chóp tứ giác đều có cạnh đáy bằng 6cm và chiều cao bằng 16cm. Thể tích của hình chóp là:

V = (1/3) * 6 * 6 * 16 = 192 (cm^3)

Alt text: Hình ảnh ví dụ về hình chóp tứ giác đều có cạnh đáy 6cm và chiều cao 16cm để minh họa tính thể tích.

III. Bài Tập Vận Dụng

Dưới đây là một số bài tập vận dụng giúp bạn củng cố kiến thức về hình chóp đều có đáy là hình vuông:

Bài 1: Cho hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao một mặt bên bằng 5cm. Tính diện tích xung quanh của hình chóp.

Giải:

Nửa chu vi đáy là: p = 2 * 4 = 8 cm

Diện tích xung quanh là: Sxq = p d = 8 5 = 40 cm²

Bài 2: Cho hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao của hình chóp là 9cm. Tính thể tích của hình chóp.

Giải:

Diện tích đáy là: Sđáy = 4 * 4 = 16 cm²

Thể tích của hình chóp là: V = (1/3) 16 9 = 48 cm³

Bài 3: Một hình chóp tứ giác đều có thể tích bằng 50cm³, chiều cao hình chóp bằng 6cm. Tính diện tích đáy của hình chóp.

Giải:

Diện tích đáy là: Sđáy = (3 V) / h = (3 50) / 6 = 25 cm²

Alt text: Hình ảnh minh họa hình chóp tứ giác đều S.ABCD với các thông số để giải bài tập, giúp người học dễ hình dung.

IV. Ứng Dụng Thực Tế

Hình chóp đều có đáy là hình vuông xuất hiện nhiều trong thực tế, ví dụ như:

• Kiến trúc: Mái nhà, chóp của các công trình kiến trúc.
• Đồ vật: Các vật trang trí, đồ chơi.

Việc nắm vững kiến thức về hình chóp đều có đáy là hình vuông không chỉ giúp bạn giải quyết các bài toán hình học mà còn giúp bạn hiểu rõ hơn về thế giới xung quanh.