Parabol là một trong những đường cong quan trọng trong toán học và có nhiều ứng dụng thực tế. Bài viết này sẽ cung cấp một cái nhìn toàn diện về cách Viết Phương Trình Parabol, từ định nghĩa cơ bản đến các dạng bài tập nâng cao và phương pháp giải chi tiết.
1. Định Nghĩa và Các Yếu Tố Của Parabol
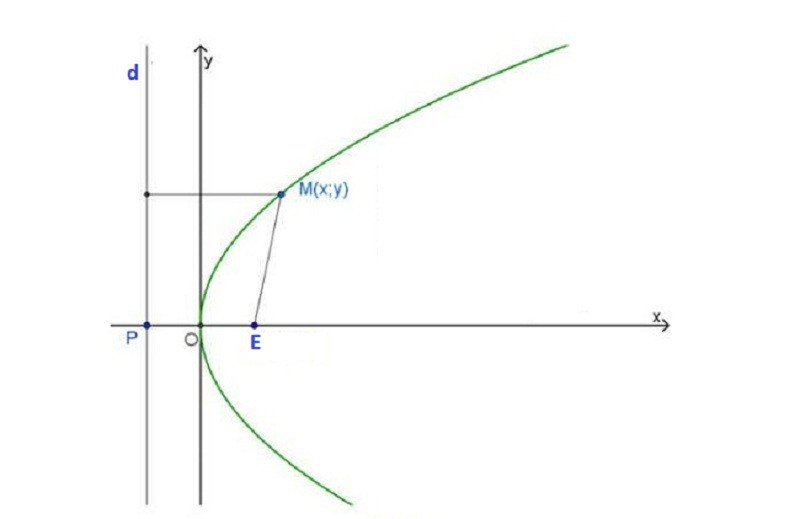
Parabol là tập hợp các điểm trong mặt phẳng cách đều một điểm cố định (tiêu điểm) và một đường thẳng cố định (đường chuẩn) không đi qua tiêu điểm.
Các yếu tố chính của một parabol bao gồm:
- Tiêu điểm (F): Điểm cố định.
- Đường chuẩn (d): Đường thẳng cố định.
- Đỉnh (V): Điểm nằm trên parabol và là trung điểm của đoạn vuông góc nối tiêu điểm với đường chuẩn.
- Trục đối xứng: Đường thẳng đi qua tiêu điểm và vuông góc với đường chuẩn.
2. Các Dạng Phương Trình Parabol
Có hai dạng phương trình parabol phổ biến: phương trình tổng quát và phương trình chính tắc. Việc nắm vững cách viết phương trình parabol ở cả hai dạng này là rất quan trọng.
2.1. Phương Trình Tổng Quát
Phương trình tổng quát của parabol có dạng:
y = ax² + bx + c
Trong đó:
a,b, vàclà các hằng số, vớia ≠ 0.- Tọa độ đỉnh của parabol là
(-b/2a; -Δ/4a), vớiΔ = b² - 4ac. - Dấu của hệ số
aquyết định hướng của parabol:- Nếu
a > 0: Parabol hướng lên trên (bề lõm hướng lên). - Nếu
a < 0: Parabol hướng xuống dưới (bề lõm hướng xuống).
- Nếu
2.2. Phương Trình Chính Tắc
Phương trình chính tắc của parabol có dạng đơn giản hơn:
y² = 2px (với p > 0)
Trong đó:
plà tham số tiêu, là khoảng cách từ tiêu điểm đến đường chuẩn.- Tiêu điểm của parabol là
(p/2; 0). - Đường chuẩn của parabol là
x = -p/2. - Đỉnh của parabol nằm tại gốc tọa độ
(0; 0).
3. Các Bước Viết Phương Trình Parabol
3.1. Xác Định Dạng Phương Trình
Trước khi bắt đầu viết phương trình parabol, bạn cần xác định dạng phương trình phù hợp với thông tin đã cho. Nếu bạn biết đỉnh và một điểm khác trên parabol, phương trình tổng quát có thể hữu ích. Nếu bạn biết tiêu điểm và đường chuẩn, phương trình chính tắc có thể đơn giản hơn.
3.2. Sử Dụng Thông Tin Đã Cho
Sử dụng các thông tin đã cho (ví dụ: tọa độ đỉnh, tiêu điểm, đường chuẩn, điểm đi qua) để thiết lập các phương trình và giải hệ phương trình để tìm các hệ số cần thiết.
3.3. Kiểm Tra và Kết Luận
Sau khi tìm được phương trình, hãy kiểm tra lại bằng cách thay các giá trị đã biết vào phương trình để đảm bảo tính chính xác. Cuối cùng, viết phương trình parabol hoàn chỉnh.
4. Các Dạng Bài Tập Viết Phương Trình Parabol và Phương Pháp Giải
Dưới đây là một số dạng bài tập thường gặp liên quan đến việc viết phương trình parabol, cùng với phương pháp giải chi tiết:
4.1. Viết Phương Trình Parabol Khi Biết Đỉnh và Một Điểm Khác
Ví dụ: Viết phương trình parabol có đỉnh I(1; -2) và đi qua điểm A(2; -1).
Giải:
- Chọn dạng phương trình: Vì biết đỉnh, ta sử dụng phương trình tổng quát:
y = a(x - h)² + k, với(h; k)là tọa độ đỉnh. - Thay tọa độ đỉnh:
y = a(x - 1)² - 2. - Thay tọa độ điểm A:
-1 = a(2 - 1)² - 2. Giải phương trình này để tìma = 1. - Viết phương trình:
y = (x - 1)² - 2 = x² - 2x - 1.
4.2. Viết Phương Trình Parabol Khi Biết Tiêu Điểm và Đường Chuẩn
Ví dụ: Viết phương trình parabol có tiêu điểm F(2; 0) và đường chuẩn x = -2.
Giải:
- Chọn dạng phương trình: Vì biết tiêu điểm và đường chuẩn, ta sử dụng phương trình chính tắc:
y² = 2px. - Tìm tham số tiêu p: Khoảng cách từ tiêu điểm đến đường chuẩn là
p = 2 - (-2) = 4. - Viết phương trình:
y² = 2 * 4 * x = 8x.
4.3. Viết Phương Trình Parabol Khi Biết Ba Điểm Thuộc Parabol
Ví dụ: Viết phương trình parabol đi qua ba điểm A(1; 1), B(-1; 5), và C(2; 8).
Giải:
- Chọn dạng phương trình: Sử dụng phương trình tổng quát:
y = ax² + bx + c. - Thiết lập hệ phương trình: Thay tọa độ ba điểm vào phương trình, ta có hệ:
a + b + c = 1a - b + c = 54a + 2b + c = 8
- Giải hệ phương trình: Giải hệ này, ta tìm được
a = 1,b = -2, vàc = 2. - Viết phương trình:
y = x² - 2x + 2.
5. Ứng Dụng Của Parabol
Parabol có nhiều ứng dụng trong thực tế, bao gồm:
- Thiết kế ăng-ten parabol: Tập trung sóng tại tiêu điểm.
- Thiết kế đèn pha: Tạo ra chùm sáng song song.
- Xây dựng cầu: Phân bổ lực đều lên các trụ.
- Quỹ đạo của vật ném xiên: Mô tả chuyển động của vật dưới tác dụng của trọng lực.
6. Kết Luận
Việc viết phương trình parabol là một kỹ năng quan trọng trong toán học. Bằng cách nắm vững định nghĩa, các dạng phương trình, và phương pháp giải bài tập, bạn có thể dễ dàng giải quyết các bài toán liên quan đến parabol và hiểu rõ hơn về ứng dụng của nó trong thực tế. Hy vọng bài viết này đã cung cấp cho bạn một hướng dẫn chi tiết và dễ hiểu.