1. Định Nghĩa và Tính Chất của Vecto Pháp Tuyến
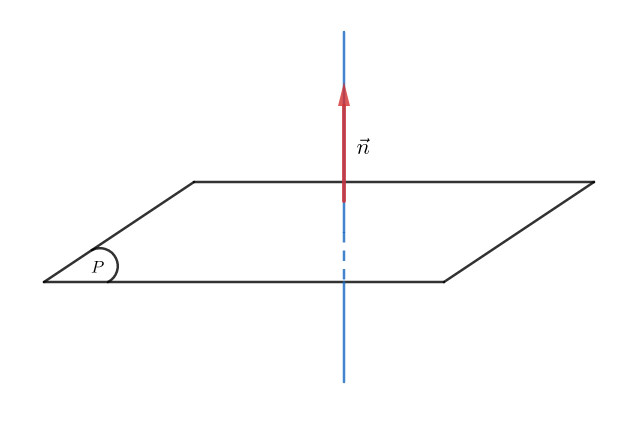
Trong không gian Oxyz, một vecto pháp tuyến của một mặt phẳng là một vecto khác vecto không, có phương vuông góc với mặt phẳng đó. Vecto pháp tuyến đóng vai trò then chốt trong việc xác định và biểu diễn mặt phẳng trong không gian ba chiều.
Hình ảnh minh họa vecto pháp tuyến vuông góc với mặt phẳng, thể hiện trực quan mối quan hệ giữa vecto và mặt phẳng.
Tính chất quan trọng:
- Nếu $overrightarrow{n}$ là một vecto pháp tuyến của mặt phẳng (P), thì $koverrightarrow{n}$ (với $k neq 0$) cũng là một vecto pháp tuyến của (P). Điều này có nghĩa là một mặt phẳng có vô số vecto pháp tuyến, chúng cùng phương với nhau.
- Một mặt phẳng hoàn toàn được xác định nếu biết một điểm thuộc mặt phẳng và một vecto pháp tuyến của nó.
2. Phương Trình Mặt Phẳng và Vecto Pháp Tuyến
2.1. Phương trình tổng quát của mặt phẳng:
Mặt phẳng (P) có vecto pháp tuyến $overrightarrow{n} = (A, B, C)$ và đi qua điểm $M_0(x_0, y_0, z_0)$ có phương trình tổng quát:
$A(x – x_0) + B(y – y_0) + C(z – z_0) = 0$
Khai triển phương trình trên, ta được:
$Ax + By + Cz + D = 0$
Trong đó, $D = -Ax_0 – By_0 – Cz_0$.
Lưu ý: Vecto $overrightarrow{n} = (A, B, C)$ chính là vecto pháp tuyến của mặt phẳng có phương trình $Ax + By + Cz + D = 0$.
2.2. Phương trình mặt phẳng theo đoạn chắn:
Mặt phẳng đi qua ba điểm $M(a, 0, 0)$, $N(0, b, 0)$, và $P(0, 0, c)$ (với $abc neq 0$) có phương trình:
$frac{x}{a} + frac{y}{b} + frac{z}{c} = 1$
Phương trình này được gọi là phương trình mặt phẳng theo đoạn chắn.
3. Xác Định Vecto Pháp Tuyến trong Các Trường Hợp Đặc Biệt
3.1. Mặt phẳng đi qua ba điểm không thẳng hàng:
Cho ba điểm $A, B, C$ không thẳng hàng. Vecto pháp tuyến của mặt phẳng (ABC) có thể được xác định bằng tích có hướng của hai vecto $overrightarrow{AB}$ và $overrightarrow{AC}$:
$overrightarrow{n} = left [ overrightarrow{AB}, overrightarrow{AC} right ]$
3.2. Mặt phẳng vuông góc với một đường thẳng:
Nếu mặt phẳng (P) vuông góc với đường thẳng d có vecto chỉ phương $overrightarrow{u}$, thì $overrightarrow{u}$ chính là vecto pháp tuyến của mặt phẳng (P).
3.3. Mặt phẳng song song với hai đường thẳng:
Nếu mặt phẳng (P) song song với hai đường thẳng $d_1$ và $d_2$ có các vecto chỉ phương lần lượt là $overrightarrow{u_1}$ và $overrightarrow{u_2}$, thì vecto pháp tuyến của (P) có thể được xác định bằng tích có hướng:
$overrightarrow{n} = left [ overrightarrow{u_1}, overrightarrow{u_2} right ]$
4. Ứng Dụng của Vecto Pháp Tuyến
4.1. Xác định vị trí tương đối giữa hai mặt phẳng:
Cho hai mặt phẳng $(P_1): A_1x + B_1y + C_1z + D_1 = 0$ và $(P_2): A_2x + B_2y + C_2z + D_2 = 0$. Vecto pháp tuyến của chúng lần lượt là $overrightarrow{n_1} = (A_1, B_1, C_1)$ và $overrightarrow{n_2} = (A_2, B_2, C_2)$.
Hình ảnh tóm tắt điều kiện để hai mặt phẳng song song, trùng nhau, cắt nhau, vuông góc dựa vào tỉ lệ và tích vô hướng của các hệ số.
- $(P_1)$ song song $(P_2)$ khi và chỉ khi $overrightarrow{n_1}$ và $overrightarrow{n_2}$ cùng phương (tức là $frac{A_1}{A_2} = frac{B_1}{B_2} = frac{C_1}{C_2} neq frac{D_1}{D_2}$).
- $(P_1)$ trùng $(P_2)$ khi và chỉ khi $overrightarrow{n_1}$ và $overrightarrow{n_2}$ cùng phương và $frac{A_1}{A_2} = frac{B_1}{B_2} = frac{C_1}{C_2} = frac{D_1}{D_2}$.
- $(P_1)$ cắt $(P_2)$ khi và chỉ khi $overrightarrow{n_1}$ và $overrightarrow{n_2}$ không cùng phương.
- $(P_1)$ vuông góc $(P_2)$ khi và chỉ khi $overrightarrow{n_1} cdot overrightarrow{n_2} = A_1A_2 + B_1B_2 + C_1C_2 = 0$.
4.2. Tính góc giữa hai mặt phẳng:
Góc $theta$ giữa hai mặt phẳng $(P_1)$ và $(P_2)$ được tính theo công thức:
$cos(theta) = frac{|overrightarrow{n_1} cdot overrightarrow{n_2}|}{|overrightarrow{n_1}| cdot |overrightarrow{n_2}|} = frac{|A_1A_2 + B_1B_2 + C_1C_2|}{sqrt{A_1^2 + B_1^2 + C_1^2} cdot sqrt{A_2^2 + B_2^2 + C_2^2}}$
Hình ảnh minh họa công thức tính cosin góc giữa hai mặt phẳng, sử dụng tích vô hướng và độ dài của các vecto pháp tuyến.
4.3. Tính khoảng cách từ một điểm đến một mặt phẳng:
Khoảng cách từ điểm $M(x_0, y_0, z_0)$ đến mặt phẳng $(P): Ax + By + Cz + D = 0$ được tính theo công thức:
$d(M, (P)) = frac{|Ax_0 + By_0 + Cz_0 + D|}{sqrt{A^2 + B^2 + C^2}}$
Hình ảnh minh họa công thức tính khoảng cách từ một điểm đến mặt phẳng, nhấn mạnh vai trò của vecto pháp tuyến trong công thức.
5. Các Dạng Bài Tập Thường Gặp và Phương Pháp Giải
5.1. Viết phương trình mặt phẳng đi qua một điểm và có vecto pháp tuyến cho trước:
- Bước 1: Xác định tọa độ điểm $M_0(x_0, y_0, z_0)$ và vecto pháp tuyến $overrightarrow{n} = (A, B, C)$.
- Bước 2: Áp dụng công thức phương trình mặt phẳng: $A(x – x_0) + B(y – y_0) + C(z – z_0) = 0$.
5.2. Viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng:
- Bước 1: Xác định tọa độ ba điểm $A, B, C$.
- Bước 2: Tính hai vecto $overrightarrow{AB}$ và $overrightarrow{AC}$.
- Bước 3: Tính tích có hướng $overrightarrow{n} = left [ overrightarrow{AB}, overrightarrow{AC} right ]$. Vecto $overrightarrow{n}$ là vecto pháp tuyến của mặt phẳng.
- Bước 4: Chọn một trong ba điểm $A, B, C$ (ví dụ điểm A) và áp dụng công thức phương trình mặt phẳng: $A(x – x_A) + B(y – y_A) + C(z – z_A) = 0$.
5.3. Viết phương trình mặt phẳng thỏa mãn điều kiện song song hoặc vuông góc:
- Điều kiện song song: Hai mặt phẳng song song có cùng vecto pháp tuyến (hoặc vecto pháp tuyến của mặt phẳng này là bội của vecto pháp tuyến của mặt phẳng kia).
- Điều kiện vuông góc: Tích vô hướng của hai vecto pháp tuyến bằng 0.
5.4. Bài toán liên quan đến khoảng cách:
Sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng để giải quyết các bài toán tìm điểm, tìm mặt phẳng thỏa mãn điều kiện khoảng cách cho trước.
6. Kết Luận
Vecto pháp tuyến là một khái niệm cơ bản và quan trọng trong hình học không gian Oxyz. Việc nắm vững lý thuyết và các ứng dụng của vecto pháp tuyến giúp giải quyết nhiều bài toán liên quan đến mặt phẳng, từ đó xây dựng nền tảng vững chắc cho việc học tập và nghiên cứu toán học. Hãy luyện tập thường xuyên để thành thạo các kỹ năng và tự tin chinh phục các bài toán hình học không gian.