Tổng của Hai Vecto
Định nghĩa tổng của hai vecto
Tổng của hai vecto là một khái niệm cơ bản trong hình học vecto, được sử dụng rộng rãi trong nhiều lĩnh vực của toán học và vật lý.
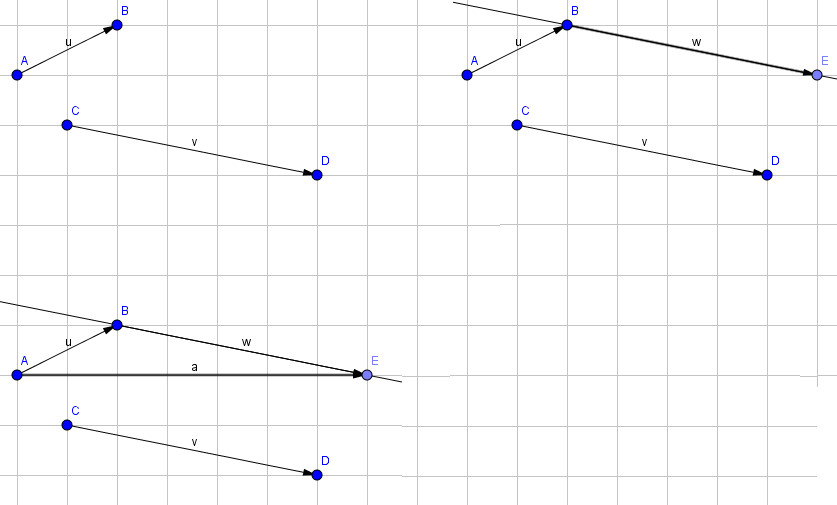
Để cộng hai vecto, ta thực hiện như sau:
- Chọn một điểm gốc A.
- Vẽ vecto AB bằng vecto a.
- Từ điểm B, vẽ vecto BC bằng vecto b.
- Vecto AC chính là tổng của hai vecto a và b, ký hiệu là vecto a + vecto b.
Hình ảnh minh họa phép cộng hai vecto a và b, kết quả là vecto tổng a + b, thể hiện rõ điểm gốc, điểm ngọn và hướng của các vecto.
Định nghĩa: Cho hai vecto $vec{a}$ và $vec{b}$. Lấy một điểm A, vẽ $vec{AB}=vec{a}$, $vec{BC}=vec{b}$, vecto $vec{AC}$ được gọi là tổng của hai vecto $vec{a}$ và $vec{b}$, tức là $vec{AC}=vec{a}+vec{b}$.
Ví dụ: Cho hình vuông ABCD, tính:
a. $vec{AB}+vec{BC}$
b. $vec{AB}+vec{CD}$
c. $vec{AB}+vec{DC}$
Hình ảnh minh họa hình vuông ABCD, ví dụ cụ thể về cộng vecto, các mũi tên chỉ hướng của vecto trên từng cạnh hình vuông.
Lời giải:
a. $vec{AB}+vec{BC}=vec{AC}$
b. $vec{AB}+vec{CD}=vec{AB}+vec{BA}=vec{AA}=vec{0}$
c. Dựng $vec{BE}=vec{DC}$, khi đó B là trung điểm AE. Vậy $vec{AB}+vec{DC}=vec{AB}+vec{BE}=vec{AE}$
Tính chất của tổng các vecto
Tổng của hai vecto có các tính chất quan trọng sau:
- Tính giao hoán: $vec{a}+vec{b}=vec{b}+vec{a}$
- Tính kết hợp: $(vec{a}+vec{b})+vec{c}=vec{a}+(vec{b}+vec{c})$
- Tính chất của vecto không: $vec{a}+vec{0}=vec{0}+vec{a}=vec{a}$
Quy tắc hình bình hành
Quy tắc hình bình hành là một trường hợp đặc biệt của tổng hai vecto, thường được sử dụng khi hai vecto có chung điểm gốc.
Quy tắc: Nếu ABCD là hình bình hành, thì $vec{AB}+vec{AD}=vec{AC}$.
Hình ảnh minh họa quy tắc hình bình hành, vecto AC là tổng của vecto AB và vecto AD, làm rõ mối quan hệ hình học.
Ví dụ 1: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Chứng minh rằng: $vec{SA}+vec{SC}=vec{SB}+vec{SD}$
Hình ảnh minh họa hình chóp S.ABCD, đáy là hình bình hành, các vecto nối từ đỉnh S đến các đỉnh đáy được thể hiện rõ ràng.
Lời giải:
Hình ảnh phân tích các vecto trong hình chóp, giải thích chi tiết cách áp dụng quy tắc hình bình hành để chứng minh đẳng thức.
Ví dụ 2: Cho hình bình hành ABCD tâm I. Khẳng định nào sau đây là sai?
- $vec{IA}+vec{IC}=0$
- $vec{AB}=vec{DC}$
- $vec{AC}=vec{BD}$
- $vec{AB}+vec{AD}=vec{AC}$
Hình ảnh minh họa hình bình hành ABCD với tâm I, các vecto liên quan được đánh dấu để phân tích và tìm ra khẳng định sai.
Lời giải:
Hình ảnh phân tích từng khẳng định, chỉ ra rằng khẳng định $vec{AC}=vec{BD}$ là sai trong trường hợp hình bình hành.
Ứng Dụng của Vecto a Cộng Vecto b
- Trung điểm của đoạn thẳng: I là trung điểm của đoạn thẳng AB khi và chỉ khi $vec{IA}+vec{IB}=vec{0}$.
- Trọng tâm của tam giác: G là trọng tâm của tam giác MNP khi và chỉ khi $vec{GM}+vec{GN}+vec{GP}=vec{0}$.
- Tính chất của vecto không: $vec{AB}+vec{0}=vec{0}+vec{AB}=vec{AB}$.
Các Dạng Bài Tập Về Tổng Vecto
Xác định độ dài tổng của 2 vecto
Phương pháp giải: Đưa tổng của các vecto về một vecto có độ dài là một cạnh của đa giác để tính độ dài của vecto.
Ví dụ: Cho hình chữ nhật ABCD. Biết AB = 4a, AD = 2a. Tính: $left | vec{AB}+vec{AD}right |$
Hình ảnh minh họa hình chữ nhật ABCD, xác định độ dài các cạnh và vecto để tính độ dài vecto tổng.
Lời giải:
$vec{AB}+vec{AD}=vec{AC}$ (quy tắc hình bình hành)
$Rightarrow left | vec{AB}+vec{AD}right|=left | vec{AC} right |=AC$
Vì ABCD là hình chữ nhật nên BC = AD = 2a
Xét tam giác ABC vuông tại B, áp dụng định lý Py-ta-go:
$AC^{2}=left ( 4a right )^{2}+left ( 2a right )^{2}=20a^{2}$
$Rightarrow AC=sqrt{20a^{2}}=2sqrt{5}a$
Chứng minh các đẳng thức vecto
Phương pháp giải: Áp dụng quy tắc ba điểm, quy tắc hình bình hành, trọng tâm, trung điểm để biến đổi vế này thành vế kia của đẳng thức hoặc biến đổi cả hai vế để được hai vế bằng nhau, hoặc biến đổi đẳng thức vecto cần chứng minh tương đương với một đẳng thức vecto đã được công nhận là đúng.
Ví dụ: Cho sáu điểm tùy ý A, B, C, D, E, F. Chứng minh đẳng thức sau:
$vec{AD}+vec{BE}+vec{CF}=vec{AE}+vec{BF}+vec{CD}$
Lời giải:
Áp dụng quy tắc ba điểm: $vec{AD}=vec{AC}+vec{CD}$
Vế trái: $vec{AD}+vec{BE}+vec{CF}=vec{AC}+vec{CD}+vec{BE}+vec{CF}=(vec{AC}+vec{CF})+vec{CD}+vec{BE}=vec{AF}+vec{CD}+vec{BE}$
Áp dụng quy tắc ba điểm: $vec{AF}=vec{AE}+vec{EF}$
Vế phải: $vec{AE}+vec{EF}+vec{CD}+vec{BE}=vec{AE}+(vec{BE}+vec{EF})+vec{CD}=vec{AE}+vec{BF}+vec{CD}$ = Vế trái (điều phải chứng minh).