Để vẽ đồ thị hàm số y=2x², chúng ta cần xác định một số điểm thuộc đồ thị và vẽ đường cong đi qua các điểm đó. Hàm số y=2x² là một hàm số bậc hai, đồ thị của nó là một parabol có đỉnh tại gốc tọa độ (0;0).
1. Lập Bảng Giá Trị:
Bước đầu tiên là tạo một bảng giá trị để xác định tọa độ của một số điểm thuộc đồ thị. Chọn các giá trị x khác nhau, tính giá trị y tương ứng bằng công thức y = 2x².
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y=2x² | 8 | 2 | 0 | 2 | 8 |
2. Xác Định Các Điểm Trên Mặt Phẳng Tọa Độ:
Từ bảng giá trị, ta có các điểm sau: A(-2; 8), B(-1; 2), O(0; 0), B'(1; 2), A'(2; 8). Đánh dấu các điểm này trên mặt phẳng tọa độ Oxy.
3. Vẽ Parabol:
Nối các điểm đã đánh dấu bằng một đường cong trơn. Đường cong này là một parabol, có đỉnh tại gốc tọa độ O(0; 0) và hướng lên trên. Do hệ số a = 2 > 0 nên parabol có bề lõm hướng lên.
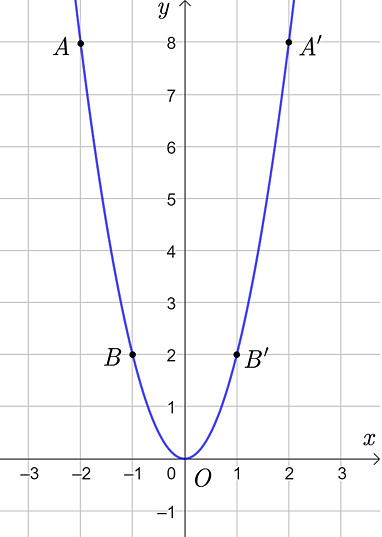Đồ thị hàm số y=2x^2 với các điểm được xác định rõ ràng
4. Nhận Xét:
- Đồ thị hàm số y=2x² là một parabol.
- Đỉnh của parabol là gốc tọa độ O(0; 0).
- Parabol đối xứng qua trục Oy.
- Khi x tăng (hoặc giảm) từ 0, giá trị y tăng nhanh chóng. Điều này do hệ số 2 nhân với x², làm cho đồ thị “dốc” hơn so với đồ thị y=x².
5. Các Bước Chi Tiết Để Vẽ Đồ Thị Chính Xác:
- Chọn tỉ lệ thích hợp: Chọn tỉ lệ trên trục x và trục y sao cho các điểm dễ dàng được biểu diễn trên giấy hoặc phần mềm vẽ đồ thị.
- Vẽ trục tọa độ: Vẽ trục x và trục y vuông góc với nhau.
- Đánh dấu các điểm: Đánh dấu chính xác các điểm đã tính toán từ bảng giá trị.
- Vẽ đường cong: Nối các điểm bằng một đường cong mượt mà. Chú ý đến tính đối xứng của parabol.
- Kiểm tra lại: Kiểm tra lại đồ thị để đảm bảo nó đi qua tất cả các điểm đã đánh dấu và có hình dạng parabol chính xác.
Lưu ý: Việc chọn nhiều điểm hơn (ví dụ như x = -1.5, -0.5, 0.5, 1.5) sẽ giúp vẽ đồ thị chính xác hơn, đặc biệt là phần đường cong.
Ứng dụng của việc vẽ đồ thị hàm số y = 2x²:
Việc hiểu và vẽ được đồ thị hàm số y = 2x² là nền tảng quan trọng trong toán học và có nhiều ứng dụng thực tế, ví dụ:
- Vật lý: Mô tả chuyển động của vật thể dưới tác dụng của trọng lực (chuyển động ném xiên, ném thẳng đứng).
- Kỹ thuật: Thiết kế các bộ phận có hình dạng parabol (ăng-ten, gương phản xạ).
- Kinh tế: Mô hình hóa một số quá trình tăng trưởng hoặc suy giảm.
Nắm vững cách vẽ đồ thị hàm số y = 2x² giúp bạn hiểu sâu hơn về hàm số bậc hai và ứng dụng của nó trong nhiều lĩnh vực khác nhau.
