Vận Tốc Bằng 0 Khi Nào: Giải Thích Chi Tiết và Bài Tập Ứng Dụng

Vận tốc là một khái niệm quan trọng trong vật lý, mô tả sự thay đổi vị trí của một vật theo thời gian. Vận tốc bằng 0 là một trạng thái đặc biệt, xảy ra khi vật đứng yên hoặc tại những thời điểm chuyển động thay đổi hướng. Bài viết này sẽ đi sâu vào các trường hợp vận tốc bằng 0, đặc biệt trong dao động điều hòa, cùng với các ví dụ và bài tập minh họa.

Các Trường Hợp Vận Tốc Bằng 0

Vận tốc của một vật bằng 0 khi:

• Vật đứng yên: Đây là trường hợp đơn giản nhất. Nếu một vật không di chuyển so với hệ quy chiếu, vận tốc của nó bằng 0. Ví dụ, một chiếc xe đang đậu, một quyển sách nằm trên bàn.
• Vật đổi hướng chuyển động: Khi một vật chuyển động theo một hướng, sau đó dừng lại và đổi hướng, tại thời điểm chuyển hướng, vận tốc của vật bằng 0. Ví dụ, một quả bóng được ném lên cao. Tại điểm cao nhất của quỹ đạo, trước khi rơi xuống, vận tốc của quả bóng bằng 0.
• Trong dao động điều hòa: Đây là trường hợp phổ biến và thú vị, đặc biệt trong các bài toán vật lý. Vật dao động điều hòa liên tục thay đổi vận tốc và hướng chuyển động.

Vận Tốc Bằng 0 Trong Dao Động Điều Hòa

Dao động điều hòa là một loại chuyển động tuần hoàn, trong đó vật di chuyển qua lại quanh một vị trí cân bằng. Vận tốc của vật trong dao động điều hòa thay đổi liên tục và đạt giá trị 0 tại các vị trí biên.

Xét một vật dao động điều hòa với phương trình:

x = Acos(ωt + φ)

Trong đó:

• x là li độ của vật tại thời điểm t.
• A là biên độ dao động.
• ω là tần số góc.
• φ là pha ban đầu.

Vận tốc của vật là đạo hàm của li độ theo thời gian:

v = -Aωsin(ωt + φ)

Vận tốc v = 0 khi sin(ωt + φ) = 0. Điều này xảy ra khi:

ωt + φ = kπ (với k là số nguyên: 0, ±1, ±2, …)

Do đó, thời điểm vận tốc bằng 0 là:

t = (kπ - φ) / ω

Tại những thời điểm này, vật ở vị trí biên của dao động.

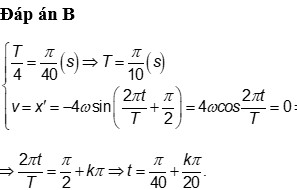Đồ thị dao động điều hòa, vận tốc bằng 0 ở biên

Hình ảnh minh họa đồ thị dao động điều hòa, thể hiện vận tốc bằng không tại các vị trí biên.

Bài Tập Vận Dụng

Xét bài toán sau: Một vật dao động điều hòa quanh vị trí cân bằng theo phương trình x = 4cos(ωt + π/2) (cm); t tính bằng giây. Biết rằng cứ sau những khoảng thời gian π/40 (s) thì động năng lại bằng nửa cơ năng. Tại những thời điểm nào thì vật có vận tốc bằng 0 (k là số nguyên)?

Phân tích bài toán:

• Phương trình dao động: x = 4cos(ωt + π/2)
• Thời gian động năng bằng nửa cơ năng: T/8 = π/40 => T = π/5 => ω = 2π/T = 10 rad/s
• Vận tốc: v = -Aωsin(ωt + φ) = -4*10*sin(10t + π/2)

Giải:

Vận tốc bằng 0 khi:

sin(10t + π/2) = 0

10t + π/2 = kπ (với k là số nguyên)

10t = kπ - π/2

t = (kπ - π/2) / 10

t = (2k - 1)π / 20 (s)

Vậy, vận tốc bằng 0 tại các thời điểm t = (2k - 1)π / 20 giây, với k là số nguyên.

Kết Luận

Hiểu rõ khái niệm vận tốc bằng 0 và các trường hợp xảy ra giúp chúng ta giải quyết các bài toán vật lý liên quan đến chuyển động, đặc biệt là dao động điều hòa. Việc nắm vững phương trình dao động và mối liên hệ giữa li độ, vận tốc, và gia tốc là rất quan trọng. Luyện tập giải các bài tập vận dụng sẽ giúp củng cố kiến thức và kỹ năng giải toán.