Trong chương trình hình học phổ thông, các bài toán liên quan đến V Hình Chóp và thể tích của chúng luôn là một phần quan trọng. Việc nắm vững lý thuyết và các công thức tính thể tích v hình chóp là yếu tố then chốt để giải quyết các bài tập hiệu quả. Bài viết này sẽ tổng hợp kiến thức cơ bản và giới thiệu các công thức tính thể tích v hình chóp thường gặp.
Lý Thuyết Cơ Bản Về Thể Tích V Hình Chóp
Thể tích là đại lượng biểu thị lượng không gian mà một vật chiếm giữ. Đơn vị đo thể tích thường là đơn vị đo độ dài lũy thừa ba (ví dụ: mét khối, centimet khối).
Alt: Khái niệm thể tích và hình ảnh minh họa một v hình chóp, một dạng hình học không gian thường gặp trong chương trình toán học phổ thông.
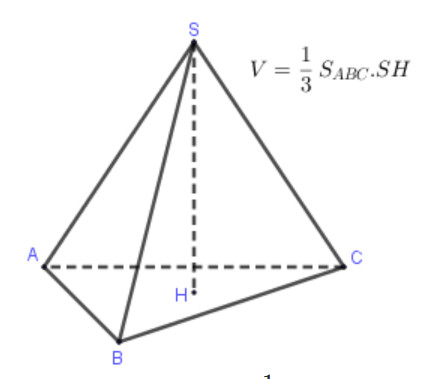
Công thức tổng quát để tính thể tích v hình chóp là:
Trong đó:
- S là diện tích mặt đáy của v hình chóp
- h là chiều cao của v hình chóp (khoảng cách từ đỉnh đến mặt đáy)
Công thức tỉ lệ thể tích thường được sử dụng trong các bài toán so sánh thể tích giữa các v hình chóp tam giác:
Alt: Công thức tính tỉ lệ thể tích giữa hai v hình chóp tam giác có chung đỉnh, sử dụng tỉ số các cạnh tương ứng.
Các Công Thức Tính Thể Tích V Hình Chóp Thường Gặp
Dưới đây là một số công thức và phương pháp tính thể tích v hình chóp thường được sử dụng trong các bài toán hình học:
V Hình Chóp Có Mặt Bên Vuông Góc Với Đáy
Nếu v hình chóp có một hoặc nhiều mặt bên vuông góc với mặt đáy, chiều cao của v hình chóp thường là đoạn vuông góc kẻ từ đỉnh xuống mặt đáy hoặc là giao tuyến của các mặt bên vuông góc với đáy.
Alt: Cách xác định đường cao trong v hình chóp khi có mặt bên vuông góc với mặt đáy, giúp tính toán thể tích chính xác.
Ví dụ: Cho v hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a; mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB=2a√3 và ∠(SBC)=30º, tính thể tích v hình chóp S.ABC.
Alt: Bài tập ví dụ về v hình chóp có mặt bên vuông góc với đáy, kèm theo hình vẽ minh họa và các thông số cụ thể.
V Hình Chóp Có Cạnh Bên Vuông Góc Với Đáy
Nếu v hình chóp có một cạnh bên vuông góc với mặt đáy, cạnh bên đó chính là chiều cao của v hình chóp.
Ví dụ: Cho v hình chóp S.ABC có SA vuông góc với đáy, SA= 4; AB= 6; BC= 10 và CA= 8. Tính thể tích v hình chóp S.ABC.
Alt: V hình chóp S.ABC có cạnh SA vuông góc đáy, ví dụ điển hình về dạng bài tập tính thể tích.
V Hình Chóp Đáy Là Hình Vuông
Đối với v hình chóp có đáy là hình vuông, diện tích đáy được tính bằng bình phương độ dài cạnh của hình vuông.
Ví dụ: Cho v hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SC tạo với mp (SAB) một góc 30 độ. Tính thể tích v hình chóp?
Thể Tích V Hình Chóp Lập Phương
Hình lập phương là trường hợp đặc biệt của v hình chóp, với tất cả các mặt là hình vuông bằng nhau. Thể tích của hình lập phương được tính bằng lập phương độ dài cạnh.
Thể Tích V Hình Chóp Lăng Trụ Tam Giác Đều
Hình lăng trụ tam giác đều là hình lăng trụ có đáy là tam giác đều và các mặt bên là hình chữ nhật. Thể tích của hình lăng trụ tam giác đều được tính bằng diện tích đáy nhân với chiều cao.
Alt: Hình ảnh minh họa bài tập tính thể tích v hình chóp lăng trụ tam giác đều, một dạng bài tập thường gặp.
Thể Tích V Hình Chóp Lục Giác Đều
V hình chóp lục giác đều là hình chóp có đáy là lục giác đều và chân đường cao trùng với tâm của lục giác đều.
Alt: V hình chóp lục giác đều với các thông số cho trước, một dạng bài toán phức tạp hơn về thể tích.
Công Thức Tính Thể Tích V Hình Chóp Lăng Trụ
Thể tích lăng trụ được tính bằng công thức: V = B.h, trong đó B là diện tích đáy và h là chiều cao của lăng trụ.
Alt: Công thức tổng quát tính thể tích v hình chóp lăng trụ, mối liên hệ giữa diện tích đáy và chiều cao.
Tính Thể Tích V Hình Chóp Khi Biết 3 Cạnh Bên
Trong trường hợp biết độ dài 6 cạnh của khối tứ diện, ta có thể sử dụng công thức tổng quát để tính thể tích.
Alt: Công thức phức tạp để tính thể tích v hình chóp tứ diện khi biết độ dài tất cả các cạnh.
Ví dụ minh họa: Cho khối tứ diện ABCD có AB=CD=8, AD=BC=5 và AC=BD=7. Thể tích khối tứ diện đã cho bằng bao nhiêu?
Alt: Ví dụ áp dụng công thức tính thể tích v hình chóp khi biết độ dài tất cả các cạnh, minh họa cách giải quyết.
Thể Tích V Hình Chóp Có Các Cạnh Đôi Một Vuông Góc
Khi các cạnh bên của v hình chóp đôi một vuông góc, thể tích được tính bằng 1/6 tích của độ dài ba cạnh đó.
Thể Tích V Hình Chóp Tròn Xoay
Thể tích v hình chóp tròn xoay (hình nón) được tính bằng công thức: V = (1/3)πr²h, trong đó r là bán kính đáy và h là chiều cao của hình nón.
Alt: V hình chóp tròn xoay (hình nón), ví dụ minh họa về tính thể tích.
Alt: Bài tập ví dụ về tính thể tích v hình chóp tròn xoay với các thông số cụ thể.
Tính Thể Tích Của V Hình Chóp Tam Giác Đều
Đây là một dạng toán thường gặp, yêu cầu xác định chiều cao và diện tích đáy một cách chính xác.
Alt: V hình chóp tam giác đều, bài tập minh họa về cách tính thể tích.
Công Thức Tính Thể Tích V Hình Chóp Tứ Giác Đều
V hình chóp tứ giác đều là hình chóp có đáy là hình vuông và chân đường cao trùng với tâm của hình vuông đó.
Alt: V hình chóp tứ giác đều với cạnh đáy bằng a, một ví dụ điển hình về tính thể tích.