Tỉ lệ nghịch là một khái niệm quan trọng trong toán học và có nhiều ứng dụng thực tế. Bài viết này sẽ cung cấp một cái nhìn toàn diện về tỉ lệ nghịch, bao gồm định nghĩa, tính chất và các dạng toán thường gặp.
Định Nghĩa Tỉ Lệ Nghịch
Hai đại lượng được gọi là tỉ lệ nghịch với nhau nếu giá trị của đại lượng này tăng thì giá trị của đại lượng kia giảm theo một tỉ lệ nhất định, sao cho tích của hai đại lượng đó luôn là một hằng số khác 0.
Cụ thể, nếu đại lượng (y) liên hệ với đại lượng (x) theo công thức:
(y = dfrac{a}{x}) hay (xy = a)
trong đó (a) là một hằng số khác 0, thì ta nói (y) tỉ lệ nghịch với (x) theo hệ số tỉ lệ (a). Ngược lại, (x) cũng tỉ lệ nghịch với (y) theo hệ số tỉ lệ (a).
Ví dụ:
Nếu (y = dfrac{5}{x}), thì (y) tỉ lệ nghịch với (x) theo hệ số tỉ lệ là 5.
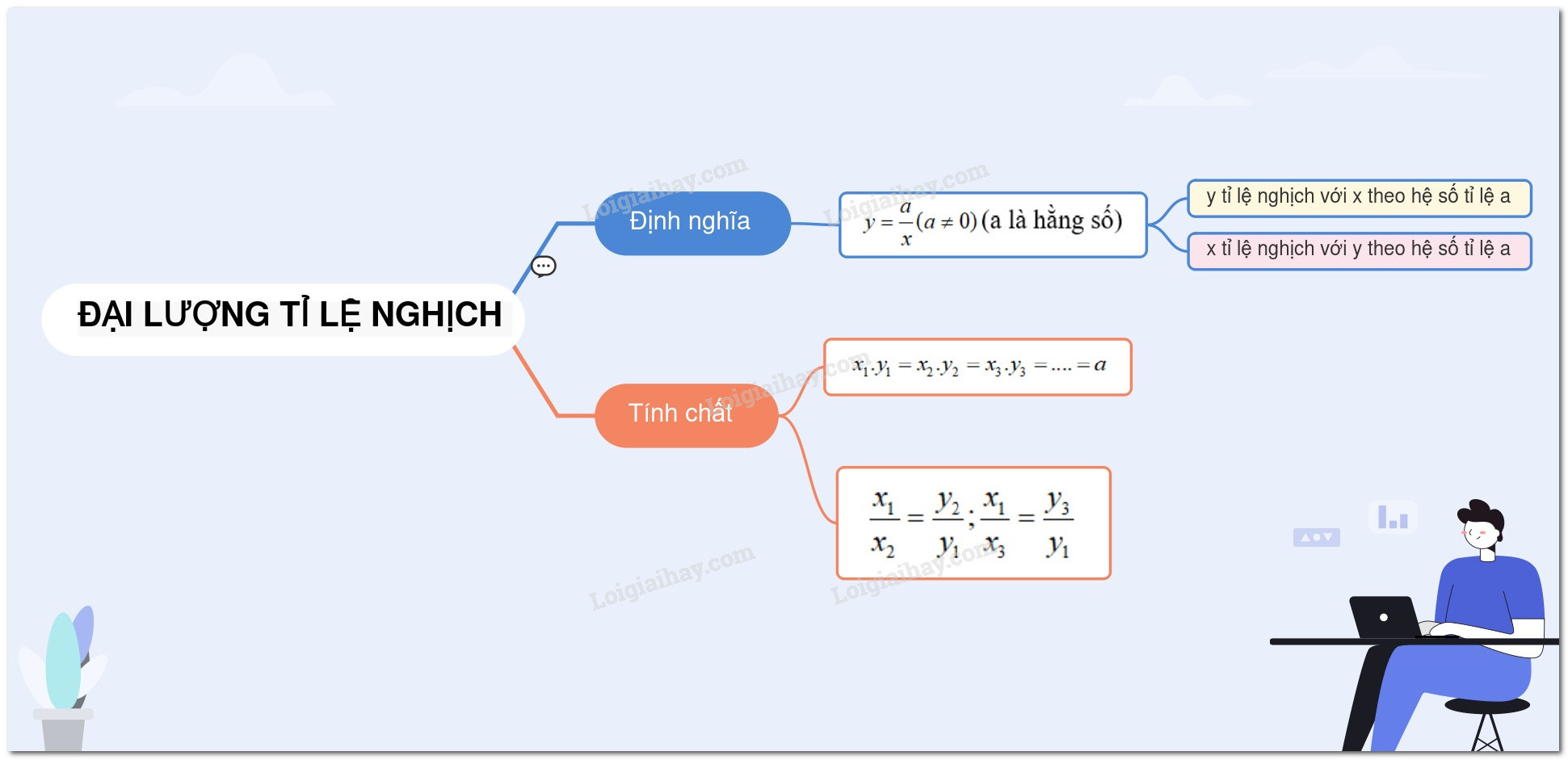Ví dụ về mối quan hệ tỉ lệ nghịch giữa x và y khi xy = a
Tính Chất Quan Trọng của Tỉ Lệ Nghịch
Khi hai đại lượng tỉ lệ nghịch với nhau, chúng có những tính chất sau:
-
Tích không đổi: Tích của hai giá trị tương ứng của hai đại lượng luôn là một hằng số.
-
Tỉ số nghịch đảo: Tỉ số của hai giá trị bất kỳ của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia.
Nếu (y) và (x) tỉ lệ nghịch với nhau theo hệ số tỉ lệ (a), thì:
- ({x_1}{y_1} = {x_2}{y_2} = {x_3}{y_3} = … = a)
- (dfrac{{{x_1}}}{{{x_2}}} = dfrac{{{y_2}}}{{{y_1}}};dfrac{{{x_1}}}{{{x_3}}} = dfrac{{{y_3}}}{{{y_1}}};…)
Các Dạng Bài Tập Thường Gặp Về Tỉ Lệ Nghịch
Dưới đây là một số dạng toán phổ biến liên quan đến tỉ lệ nghịch:
1. Tìm Giá Trị Tương Ứng Trong Bảng
Phương pháp:
- Xác định hệ số tỉ lệ (a).
- Sử dụng công thức (y = dfrac{a}{x}) hoặc (x = dfrac{a}{y}) để tìm các giá trị còn thiếu.
Ví dụ:
Cho biết (x) và (y) là hai đại lượng tỉ lệ nghịch. Khi (x = 4) thì (y = 9). Tìm (y) khi (x = 6).
Giải:
Vì (x) và (y) tỉ lệ nghịch nên (xy = a) (với (a) là hằng số).
Ta có: (4 cdot 9 = a Rightarrow a = 36)
Vậy khi (x = 6), ta có: (y = dfrac{36}{6} = 6)
2. Xác Định Tương Quan Tỉ Lệ Nghịch
Phương pháp:
- Kiểm tra xem tích của các giá trị tương ứng của hai đại lượng có bằng nhau hay không.
- Nếu tất cả các tích bằng nhau, thì hai đại lượng tỉ lệ nghịch. Ngược lại, nếu có ít nhất một cặp giá trị có tích khác, thì chúng không tỉ lệ nghịch.
3. Bài Toán Ứng Dụng Thực Tế
Phương pháp:
- Xác định các đại lượng liên quan trong bài toán.
- Xác định mối quan hệ tỉ lệ nghịch giữa chúng.
- Áp dụng tính chất và công thức để giải quyết bài toán.
Ví dụ:
Một người đi xe máy từ A đến B với vận tốc 40 km/h mất 3 giờ. Nếu người đó muốn đến B trong 2 giờ, thì vận tốc phải là bao nhiêu?
Giải:
Thời gian và vận tốc là hai đại lượng tỉ lệ nghịch.
Gọi vận tốc cần tìm là (v).
Ta có: (40 cdot 3 = v cdot 2)
(Rightarrow v = dfrac{40 cdot 3}{2} = 60) km/h
Vậy vận tốc cần thiết để đến B trong 2 giờ là 60 km/h.
4. Chia Một Số Thành Các Phần Tỉ Lệ Nghịch
Phương pháp:
Giả sử cần chia số (M) thành ba phần (x, y, z) tỉ lệ nghịch với các số (a, b, c) khác 0.
Khi đó:
(ax = by = cz) hay (dfrac{x}{{dfrac{1}{a}}} = dfrac{y}{{dfrac{1}{b}}} = dfrac{z}{{dfrac{1}{c}}}.)
Điều này có nghĩa là ta cần chia số (M) thành các phần tỉ lệ thuận với các số (dfrac{1}{a}; dfrac{1}{b}; dfrac{1}{c}).
Bài Tập Vận Dụng
Bài 1: Biết rằng (x) và (y) là hai đại lượng tỉ lệ nghịch, khi (x = 5) thì (y = 8). Tính giá trị của (y) khi (x = 10).
Bài 2: Ba người cùng làm một công việc. Người thứ nhất làm xong trong 4 giờ, người thứ hai làm xong trong 6 giờ, người thứ ba làm xong trong 12 giờ. Hỏi mỗi người làm được bao nhiêu phần công việc, biết rằng tổng cộng họ làm xong công việc?
Lời giải:
Bài 1: Vì (x) và (y) tỉ lệ nghịch nên (xy = a). Ta có (5 cdot 8 = a Rightarrow a = 40). Khi (x = 10), thì (y = dfrac{40}{10} = 4).
Bài 2: Gọi (x, y, z) là phần công việc mỗi người làm được. Vì thời gian làm và phần công việc là tỉ lệ nghịch, ta có (4x = 6y = 12z) và (x + y + z = 1). Từ (4x = 6y = 12z) suy ra (dfrac{x}{{dfrac{1}{4}}} = dfrac{y}{{dfrac{1}{6}}} = dfrac{z}{{dfrac{1}{12}}}). Áp dụng tính chất dãy tỉ số bằng nhau, ta tìm được (x = dfrac{1}{2}, y = dfrac{1}{3}, z = dfrac{1}{6}).
Hiểu rõ về tỉ lệ nghịch giúp chúng ta giải quyết nhiều bài toán và ứng dụng thực tế một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về chủ đề này.
