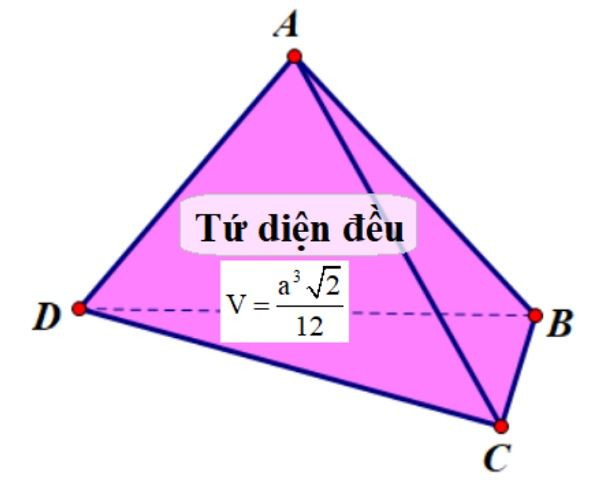
Tứ Diện Đều Là Gì? Định Nghĩa Cơ Bản
Trước khi đi sâu vào công thức tính thể tích, chúng ta cần hiểu rõ khái niệm tứ diện đều. Tứ diện đều là một loại hình chóp tam giác đặc biệt, với tất cả bốn mặt đều là tam giác đều bằng nhau. Điều này có nghĩa là tất cả các cạnh của tứ diện đều có độ dài bằng nhau, tạo nên một hình khối đối xứng và cân đối.
Công Thức Tính Thể Tích Khối Tứ Diện Đều
Công thức tính thể tích (V) của một khối tứ diện đều với cạnh có độ dài là “a” được xác định như sau:
V = (a³√2) / 12
Công thức này là nền tảng để giải quyết các bài toán liên quan đến thể tích của khối tứ diện đều. Việc hiểu và nắm vững công thức này giúp học sinh, sinh viên và những người làm trong lĩnh vực kỹ thuật dễ dàng tính toán và ứng dụng vào thực tế.
Hướng Dẫn Chi Tiết Cách Tính Thể Tích Tứ Diện Đều
Để tính thể tích khối tứ diện đều, bạn thực hiện theo các bước sau:
- Xác định độ dài cạnh (a): Tìm hiểu đề bài và xác định chính xác độ dài cạnh của khối tứ diện đều.
- Tính a³ (a mũ 3): Nhân độ dài cạnh a với chính nó ba lần (a * a * a).
- Tính √2 (căn bậc hai của 2): Sử dụng máy tính hoặc ghi nhớ giá trị gần đúng của √2 là 1.4142.
- Tính a³√2: Nhân kết quả từ bước 2 (a³) với kết quả từ bước 3 (√2).
- Chia cho 12: Chia kết quả từ bước 4 cho 12. Kết quả cuối cùng chính là thể tích của khối tứ diện đều.
Ví dụ minh họa: Cho khối tứ diện đều có cạnh a = 6 cm.
- a = 6 cm
- a³ = 6 * 6 * 6 = 216 cm³
- √2 ≈ 1.4142
- a³√2 = 216 * 1.4142 ≈ 305.57 cm³
- V = 305.57 / 12 ≈ 25.46 cm³
Vậy thể tích của khối tứ diện đều là khoảng 25.46 cm³.
Chứng Minh Công Thức Thể Tích Khối Tứ Diện Đều (a³√2) / 12
Công thức tính thể tích tứ diện đều V = (a³√2) / 12 không phải ngẫu nhiên mà có. Nó xuất phát từ việc kết hợp các kiến thức về hình học không gian, tam giác đều và định lý Pythagoras. Dưới đây là phác thảo các bước chứng minh:
-
Diện tích đáy (S): Đáy của tứ diện đều là một tam giác đều cạnh a, nên diện tích của nó là S = (a²√3) / 4.
-
Chiều cao (h): Để tìm chiều cao của tứ diện, ta kẻ đường cao từ đỉnh xuống mặt đáy. Đường cao này chia mặt đáy thành các tam giác vuông. Sử dụng định lý Pythagoras, ta có thể tính được chiều cao h = a√(2/3).
-
Thể tích (V): Thể tích của khối chóp (trong trường hợp này là tứ diện đều) được tính bằng công thức V = (1/3) S h. Thay S và h bằng các giá trị đã tính ở trên, ta có:
V = (1/3) * (a²√3 / 4) * (a√(2/3)) = (a³√2) / 12
Như vậy, công thức V = (a³√2) / 12 được chứng minh thông qua việc áp dụng các kiến thức hình học cơ bản.
Bài Tập Vận Dụng Tính Thể Tích Tứ Diện Đều
Để củng cố kiến thức, hãy cùng giải một số bài tập vận dụng sau:
Bài 1: Một khối tứ diện đều có cạnh dài 8 cm. Tính thể tích của khối tứ diện đó.
-
Giải: Áp dụng công thức V = (a³√2) / 12, với a = 8 cm.
V = (8³√2) / 12 = (512√2) / 12 ≈ 60.34 cm³
Bài 2: Cho một hình chóp tam giác đều S.ABC có cạnh đáy AB = 4 cm và chiều cao của hình chóp là 6 cm. Tính thể tích của hình chóp này. (Lưu ý: Hình chóp tam giác đều không phải là tứ diện đều).
- Giải: Bài này không áp dụng công thức tứ diện đều. Thể tích hình chóp tam giác đều là V = (1/3) Sđáy h = (1/3) (AB²√3)/4 h = (1/3) (4²√3)/4 6 = 8√3 cm³
Bài 3: Một khối tứ diện đều có thể tích là 10 cm³. Tính độ dài cạnh của khối tứ diện đó.
- Giải: Áp dụng công thức V = (a³√2) / 12. Ta có 10 = (a³√2) / 12. Suy ra a³ = (10 * 12) / √2 ≈ 84.85. Vậy a = ³√84.85 ≈ 4.39 cm
Ứng Dụng Thực Tế Của Thể Tích Tứ Diện Đều
Mặc dù có vẻ trừu tượng, kiến thức về thể tích tứ diện đều có nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực:
- Kiến trúc và xây dựng: Tính toán vật liệu xây dựng, thiết kế các cấu trúc có hình dạng tứ diện.
- Thiết kế đồ họa và game: Tạo hình các đối tượng 3D, mô phỏng các vật thể trong không gian.
- Khoa học vật liệu: Nghiên cứu cấu trúc tinh thể của vật liệu.
Kết Luận
Nắm vững công thức và cách tính thể tích khối tứ diện đều là một kỹ năng quan trọng trong hình học không gian. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn khi giải quyết các bài toán liên quan đến chủ đề này.