Tứ giác nội tiếp là một khái niệm quan trọng trong hình học phẳng, đặc biệt là chương trình Toán lớp 9. Hiểu rõ “Tứ Giác Nội Tiếp đường Tròn Khi Nào” giúp học sinh giải quyết nhiều bài toán liên quan. Bài viết này sẽ trình bày chi tiết về định nghĩa, tính chất, các dấu hiệu nhận biết và phương pháp chứng minh tứ giác nội tiếp một cách dễ hiểu và đầy đủ nhất.
Tứ Giác Nội Tiếp Là Gì?
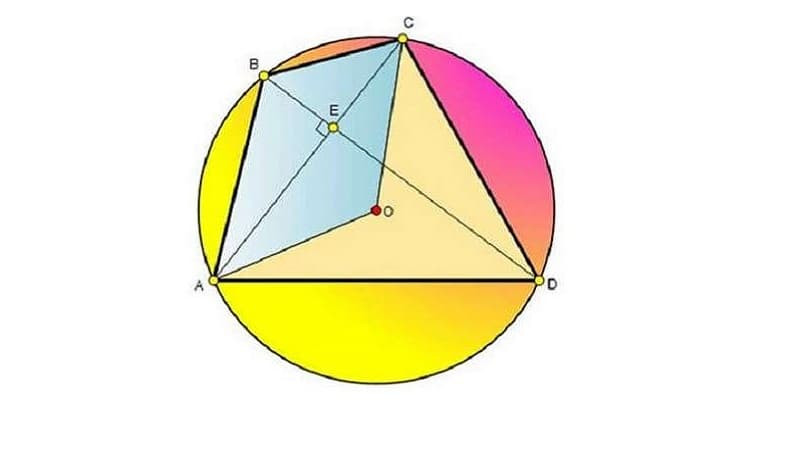
Tứ giác nội tiếp (hay tứ giác nội tiếp đường tròn) là tứ giác có bốn đỉnh cùng nằm trên một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp tứ giác.
Hình ảnh minh họa định nghĩa tứ giác nội tiếp, trong đó 4 đỉnh của tứ giác nằm trên đường tròn.
Định lý thuận: Trong một tứ giác nội tiếp, tổng hai góc đối diện bằng 180 độ.
Định lý đảo: Nếu một tứ giác có tổng hai góc đối diện bằng 180 độ thì tứ giác đó nội tiếp được trong một đường tròn.
Tính Chất Quan Trọng Của Tứ Giác Nội Tiếp
Nắm vững tính chất là yếu tố then chốt để nhận biết “tứ giác nội tiếp đường tròn khi nào”. Dưới đây là những tính chất quan trọng:
- Tổng hai góc đối diện bằng 180 độ: Đây là tính chất cơ bản nhất, được sử dụng nhiều trong các bài toán chứng minh.
- Góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện: Tính chất này cũng rất hữu ích, đặc biệt khi đề bài cho thông tin về góc ngoài.
- Mọi tam giác đều có đường tròn ngoại tiếp: Điều này suy ra từ định nghĩa tứ giác nội tiếp, vì tam giác có thể coi là một trường hợp đặc biệt của tứ giác (khi một cạnh suy biến thành điểm).
- Bốn đỉnh cách đều một điểm: Điểm này chính là tâm của đường tròn ngoại tiếp.
Dấu Hiệu Nhận Biết Tứ Giác Nội Tiếp Đường Tròn Khi Nào?
Để trả lời câu hỏi “tứ giác nội tiếp đường tròn khi nào”, ta cần nắm vững các dấu hiệu nhận biết sau:
-
Bốn đỉnh của tứ giác cách đều một điểm: Nếu tồn tại một điểm O sao cho OA = OB = OC = OD, thì tứ giác ABCD nội tiếp được trong đường tròn tâm O.
-
Tổng hai góc đối của tứ giác bằng 180 độ: Nếu ∠A + ∠C = 180° hoặc ∠B + ∠D = 180°, thì tứ giác ABCD nội tiếp.
Hình ảnh minh họa tứ giác nội tiếp có tổng hai góc đối diện bằng 180 độ, một dấu hiệu quan trọng để xác định tứ giác nội tiếp.
-
Góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện: Nếu ∠BAx (góc ngoài tại A) bằng ∠C, thì tứ giác ABCD nội tiếp.
Hình ảnh minh họa tứ giác nội tiếp, trong đó góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện, một dấu hiệu hữu ích trong chứng minh.
-
Hai đỉnh kề nhau của tứ giác cùng nhìn một cạnh dưới một góc bằng nhau: Giả sử hai đỉnh B và C cùng nhìn cạnh AD dưới góc α, thì tứ giác ABCD nội tiếp. Đây còn gọi là “quỹ tích cung chứa góc”.
-
Chứng minh thông qua các tứ giác đặc biệt: Một số hình đặc biệt như hình chữ nhật, hình vuông, hình thang cân luôn nội tiếp được trong đường tròn.
Hình ảnh minh họa các tứ giác đặc biệt (hình chữ nhật, hình vuông, hình thang cân) luôn nội tiếp được đường tròn.
Các Phương Pháp Chứng Minh Tứ Giác Nội Tiếp
Để chứng minh một tứ giác là nội tiếp, bạn có thể áp dụng một trong các phương pháp sau, dựa trên các dấu hiệu nhận biết đã nêu:
1. Chứng Minh Bốn Đỉnh Cách Đều Một Điểm
Đây là phương pháp trực tiếp, thường được sử dụng khi đề bài đã cho hoặc gợi ý về tâm đường tròn. Bạn cần chứng minh khoảng cách từ một điểm đến bốn đỉnh của tứ giác bằng nhau.
Hình ảnh minh họa cách chứng minh tứ giác nội tiếp bằng cách chứng minh bốn đỉnh cách đều một điểm cố định.
Ví dụ: Cho điểm I và tứ giác ABCD. Chứng minh IA = IB = IC = ID. Khi đó, I là tâm đường tròn ngoại tiếp tứ giác ABCD.
2. Chứng Minh Tổng Hai Góc Đối Bằng 180 Độ
Phương pháp này phổ biến và hiệu quả. Bạn cần tính toán và chứng minh tổng hai góc đối diện của tứ giác bằng 180 độ.
Ví dụ: Cho tứ giác ABCD, chứng minh ∠A + ∠C = 180° hoặc ∠B + ∠D = 180°.
3. Chứng Minh Góc Ngoài Tại Một Đỉnh Bằng Góc Trong Tại Đỉnh Đối Diện
Phương pháp này hữu ích khi đề bài cho thông tin về góc ngoài. Bạn cần chứng minh góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
Ví dụ: Chứng minh góc ngoài tại đỉnh A bằng góc trong của đỉnh C.
4. Chứng Minh Hai Đỉnh Kề Nhau Cùng Nhìn Một Cạnh Dưới Một Góc Bằng Nhau
Phương pháp này dựa trên “quỹ tích cung chứa góc”. Bạn cần chứng minh hai đỉnh kề nhau cùng nhìn một cạnh dưới cùng một góc.
Ví dụ: Chứng minh hai đỉnh B và C cùng nhìn cạnh AD dưới góc α.
5. Chứng Minh Tứ Giác Là Hình Đặc Biệt
Nếu tứ giác đã cho là hình chữ nhật, hình vuông hoặc hình thang cân, bạn có thể kết luận ngay tứ giác đó nội tiếp được trong đường tròn.
Bài Tập Vận Dụng
Để hiểu rõ hơn về cách áp dụng các dấu hiệu và phương pháp chứng minh, hãy cùng xem xét một số ví dụ sau:
Bài 1: Cho tam giác nhọn ABC, các đường cao BM và CN cắt nhau tại H. Chứng minh tứ giác AMHN và BNMC là các tứ giác nội tiếp.
Hình ảnh minh họa bài toán chứng minh tứ giác nội tiếp dựa vào đường cao trong tam giác.
Giải:
- Xét tứ giác AMHN: ∠AMH = 90° và ∠ANH = 90°. Vậy ∠AMH + ∠ANH = 180°. Suy ra AMHN là tứ giác nội tiếp (tổng hai góc đối bằng 180°).
- Xét tứ giác BNMC: ∠BNC = 90° và ∠BMC = 90°. Vậy ∠BNC + ∠BMC = 180°. Suy ra BNMC là tứ giác nội tiếp (tổng hai góc đối bằng 180°).
Bài 2: Cho tứ giác ABCD nội tiếp đường tròn (O). M là một điểm nằm trên cung AB. MD cắt AB tại E, MC cắt AB tại P. Chứng minh tứ giác PEDC nội tiếp.
Giải:
- ∠AED = 1/2 (sđ cung AD + sđ cung MB)
- ∠MCD = 1/2 sđ cung DM
- Mà sđ cung DM = sđ cung AD + sđ cung MB
- => ∠AED = ∠MCD => Tứ giác PEDC nội tiếp (góc ngoài tại 1 đỉnh bằng góc trong đỉnh đối diện)
Bài 3: Cho hình thang ABCD (AB // CD), ∠C = ∠D = 60°, CD = 2AB. Chứng minh A, B, C, D cùng nằm trên một đường tròn.
Giải:
- Gọi I là trung điểm CD => CI = AB và CI // AB => ABCI là hình bình hành => BC = AI (1)
- Chứng minh tương tự ta có AD = BI (2)
- ABCD là hình thang cân (∠C = ∠D) (3)
- Từ (1)(2)(3) => tam giác IAD và tam giác IBC đều => AI = BI = CI = DI => A, B, C, D cùng nằm trên một đường tròn.
Lưu Ý Khi Giải Bài Tập Về Tứ Giác Nội Tiếp
- Vẽ hình chính xác: Một hình vẽ đúng sẽ giúp bạn dễ dàng nhận ra các mối quan hệ hình học.
- Ghi rõ giả thiết và kết luận: Việc này giúp bạn tập trung vào mục tiêu cần chứng minh.
- Nắm vững lý thuyết: Hiểu rõ định nghĩa, tính chất và các dấu hiệu nhận biết là nền tảng để giải bài tập.
- Không sử dụng điều cần chứng minh để chứng minh: Đây là lỗi sai phổ biến mà nhiều học sinh mắc phải.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau giúp bạn làm quen với các dạng toán và rèn luyện kỹ năng chứng minh.
Kết Luận
Hiểu rõ “tứ giác nội tiếp đường tròn khi nào” là chìa khóa để giải quyết các bài toán hình học liên quan. Bằng cách nắm vững định nghĩa, tính chất, các dấu hiệu nhận biết và luyện tập thường xuyên, bạn sẽ tự tin chinh phục mọi bài toán về tứ giác nội tiếp. Chúc các bạn học tốt!