Tứ Giác đều là một khái niệm quan trọng trong hình học, đặc biệt khi nghiên cứu về hình chóp đều và các ứng dụng thực tế của nó. Bài viết này sẽ cung cấp kiến thức đầy đủ về tứ giác đều, bao gồm định nghĩa, các tính chất quan trọng, công thức tính toán liên quan và các ví dụ minh họa.
Định Nghĩa và Đặc Điểm của Tứ Giác Đều
Tứ giác đều, hay còn gọi là hình vuông, là một hình tứ giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau (đều là góc vuông 90 độ). Đây là một trường hợp đặc biệt của hình chữ nhật và hình thoi.
Hình chóp tứ giác đều là hình chóp có đáy là một tứ giác đều (hình vuông), các cạnh bên bằng nhau, và chân đường cao của hình chóp trùng với giao điểm của hai đường chéo của đáy.
Hình chóp tứ giác đều có đáy là hình vuông, 4 cạnh bên bằng nhau và các mặt bên là các tam giác cân.
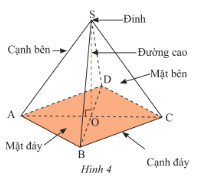
Các yếu tố cấu thành hình chóp tứ giác đều:
- Đáy: Hình vuông
- Cạnh bên: Bằng nhau
- Mặt bên: Các tam giác cân bằng nhau, chung một đỉnh
- Đường cao: Đoạn thẳng nối đỉnh của chóp với tâm của đáy (giao điểm hai đường chéo)
Công Thức Tính Diện Tích và Thể Tích Liên Quan Đến Tứ Giác Đều
Diện Tích Xung Quanh Hình Chóp Tứ Giác Đều
Diện tích xung quanh của hình chóp tứ giác đều bằng nửa chu vi đáy nhân với độ dài trung đoạn (đường cao của mặt bên).
Công thức: 𝑆xq = p.d
Trong đó:
- 𝑆xq là diện tích xung quanh
- p là nửa chu vi đáy
- d là trung đoạn
Công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Thể Tích Hình Chóp Tứ Giác Đều
Thể tích của hình chóp tứ giác đều bằng 1/3 diện tích đáy nhân với chiều cao.
Công thức: V = (1/3) Sđáy h
Trong đó:
- V là thể tích
- Sđáy là diện tích đáy (hình vuông)
- h là chiều cao của hình chóp
Công thức tính thể tích của hình chóp tứ giác đều.
Ví dụ:
Cho hình chóp tứ giác đều có cạnh đáy là 6cm và chiều cao là 16cm. Thể tích của hình chóp là: V = (1/3) 6 6 * 16 = 192 cm³.
Ví dụ minh họa cách tính thể tích hình chóp tứ giác đều.
Bài Tập Vận Dụng
Dưới đây là một số bài tập vận dụng để củng cố kiến thức về tứ giác đều và hình chóp tứ giác đều.
Bài 1: Cho hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao một mặt bên (trung đoạn) bằng 5cm. Tính diện tích xung quanh của hình chóp.
Giải:
Chu vi đáy là: 4 * 4 = 16cm
Nửa chu vi đáy là: 16 / 2 = 8cm
Diện tích xung quanh là: 8 * 5 = 40 cm²
Bài 2: Một hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao của hình chóp là 9cm. Tính thể tích của hình chóp đó.
Giải:
Diện tích đáy là: 4 * 4 = 16 cm²
Thể tích của hình chóp là: (1/3) 16 9 = 48 cm³
Bài 3: Cho khối chóp tứ giác đều, nếu tăng cạnh đáy lên ba lần và giảm chiều cao đi ba lần thì thể tích của khối chóp sẽ thay đổi như thế nào?
Giải:
Khi cạnh đáy tăng 3 lần, diện tích đáy tăng 9 lần (3 * 3). Khi chiều cao giảm 3 lần, thể tích sẽ tăng 9/3 = 3 lần. Vậy thể tích khối chóp tăng lên 3 lần.
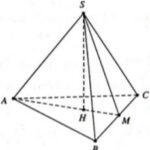
Hình ảnh minh họa cho các bài toán liên quan đến hình chóp tứ giác đều.
Ứng Dụng Thực Tế của Tứ Giác Đều
Hình chóp tứ giác đều và các tính chất của nó có nhiều ứng dụng trong thực tế, ví dụ như:
- Kiến trúc: Thiết kế mái nhà, chóp nón của các công trình.
- Xây dựng: Tính toán vật liệu xây dựng cho các công trình có hình dạng chóp.
- Đóng gói: Thiết kế các loại hộp đựng sản phẩm có hình dạng đặc biệt.
Hiểu rõ về tứ giác đều và hình chóp tứ giác đều giúp chúng ta áp dụng kiến thức hình học vào giải quyết các vấn đề thực tế một cách hiệu quả.