Site icon donghochetac

Tứ Diện Đều ABCD: Công Thức Tính Thể Tích và Ứng Dụng

donghochetacdh
Mô tả hình tứ diện đều ABCD với M là trung điểm CD và H là trọng tâm tam giác BCD để tính thể tích

Mô tả hình tứ diện đều ABCD với M là trung điểm CD và H là trọng tâm tam giác BCD để tính thể tích

Tứ Diện đều Abcd là một hình khối đa diện đặc biệt, nổi bật với tính đối xứng cao và những tính chất hình học thú vị. Việc nắm vững công thức tính thể tích và các đặc điểm của tứ diện đều ABCD là vô cùng quan trọng trong chương trình hình học không gian. Bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện về tứ diện đều ABCD, từ định nghĩa, công thức tính thể tích, đến các bài tập ứng dụng.

Tứ diện đều ABCD là hình chóp tam giác đều, có tất cả các cạnh bằng nhau và tất cả các mặt là các tam giác đều bằng nhau. Điều này dẫn đến việc tất cả các góc giữa các cạnh và các mặt của tứ diện đều bằng nhau, tạo nên một hình khối hoàn hảo về mặt hình học.

Để tính thể tích của tứ diện đều ABCD cạnh a, chúng ta có thể sử dụng công thức sau:

V = (a³√2) / 12

Công thức này được suy ra dựa trên việc xác định chiều cao của tứ diện đều và diện tích đáy (tam giác đều).

Dưới đây là cách chứng minh công thức trên:

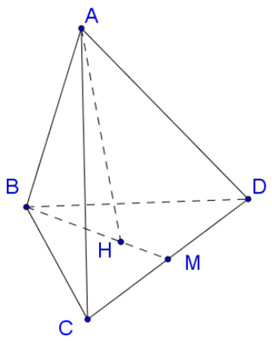
  1. Xác định trọng tâm: Gọi M là trung điểm của CD, H là trọng tâm của tam giác BCD. AH là đường cao của tứ diện đều ABCD.

  1. Tính độ dài các đoạn:

    • BM = a√3 / 2 (đường cao của tam giác đều BCD cạnh a)
    • BH = (2/3)BM = (2/3) * (a√3 / 2) = a√3 / 3

  2. Tính chiều cao AH:

    • Áp dụng định lý Pitago cho tam giác ABH vuông tại H: AH² = AB² – BH² = a² – (a√3 / 3)² = a² – a²/3 = (2/3)a²
    • Suy ra: AH = a√(2/3) = (a√6) / 3

  3. Tính diện tích đáy BCD:

    • S(BCD) = (a²√3) / 4

  4. Tính thể tích:

    • V(ABCD) = (1/3) AH S(BCD) = (1/3) (a√6 / 3) (a²√3 / 4) = (a³√2) / 12

Ví dụ: Cho tứ diện đều ABCD cạnh 6cm. Tính thể tích của tứ diện.

Giải:

Áp dụng công thức: V = (a³√2) / 12 = (6³√2) / 12 = (216√2) / 12 = 18√2 cm³

Các bài tập ứng dụng:

  1. Cho tứ diện đều ABCD cạnh a. Tính khoảng cách từ A đến mặt phẳng (BCD).
  2. Cho tứ diện đều ABCD. Tính góc giữa hai mặt phẳng (ABC) và (DBC).
  3. Một hình hộp chữ nhật có tất cả các mặt là hình vuông cạnh a. Chứng minh rằng bốn đỉnh của hình hộp tạo thành một tứ diện đều. Tính thể tích của tứ diện đều đó.

Tứ diện đều ABCD không chỉ là một khái niệm hình học đơn thuần mà còn là nền tảng để giải quyết nhiều bài toán phức tạp hơn trong không gian. Việc hiểu rõ các tính chất và công thức liên quan đến tứ diện đều ABCD sẽ giúp bạn tự tin hơn trong học tập và các kỳ thi.

Exit mobile version