Đường trung tuyến là một khái niệm quan trọng trong hình học, đặc biệt là khi nghiên cứu về tam giác. Vậy Trung Tuyến Là J? Bài viết này sẽ cung cấp định nghĩa chi tiết, công thức tính toán và các tính chất liên quan đến đường trung tuyến, giúp bạn hiểu rõ hơn về khái niệm này.
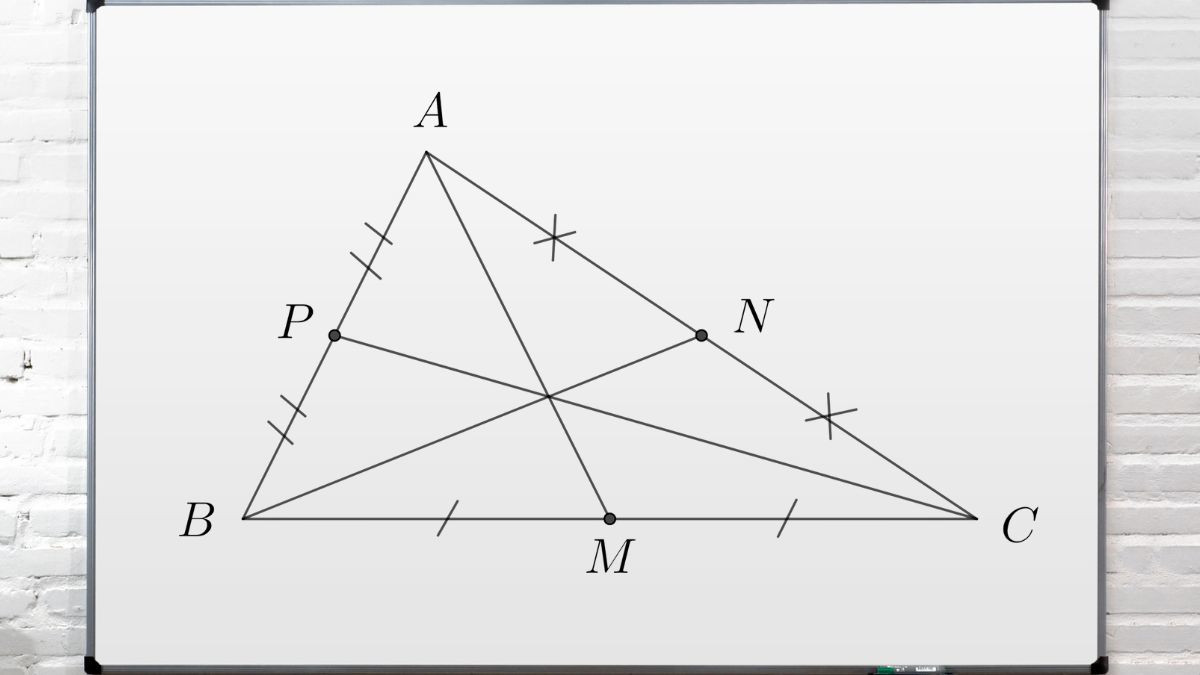
Đường trung tuyến của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng đó. Trung điểm là điểm chia đoạn thẳng thành hai phần bằng nhau. Trong một tam giác, đường trung tuyến là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến, mỗi đường ứng với một đỉnh.
Định nghĩa trực quan về đường trung tuyến trong tam giác, nối mỗi đỉnh tới trung điểm cạnh đối diện.
Công Thức Tính Độ Dài Đường Trung Tuyến
Để trả lời câu hỏi “trung tuyến là j” một cách đầy đủ, không thể bỏ qua công thức tính độ dài của nó. Cho tam giác ABC với các cạnh có độ dài lần lượt là a, b, c. Gọi ma, mb, mc lần lượt là độ dài các đường trung tuyến ứng với các cạnh a, b, c. Ta có công thức tính như sau, dựa trên định lý Apollonius:
-
Đường trung tuyến ứng với cạnh a (ma):
ma = √(2b² + 2c² - a²) / 2 -
Đường trung tuyến ứng với cạnh b (mb):
mb = √(2a² + 2c² - b²) / 2 -
Đường trung tuyến ứng với cạnh c (mc):
mc = √(2a² + 2b² - c²) / 2
Công thức này cho phép tính độ dài đường trung tuyến khi biết độ dài ba cạnh của tam giác.
Công thức toán học chi tiết để tính độ dài các đường trung tuyến trong tam giác khi biết độ dài ba cạnh.
Tính Chất Quan Trọng Của Đường Trung Tuyến
Các đường trung tuyến không chỉ đơn thuần là các đoạn thẳng nối đỉnh với trung điểm cạnh đối diện. Chúng còn có những tính chất đặc biệt:
- Đồng quy: Ba đường trung tuyến của một tam giác đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.
- Tỉ lệ: Trọng tâm chia mỗi đường trung tuyến thành hai đoạn, trong đó đoạn nối từ đỉnh đến trọng tâm dài gấp đôi đoạn nối từ trọng tâm đến trung điểm cạnh đối diện. Nói cách khác, khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng ⅔ đường trung tuyến tương ứng với đỉnh đó, và khoảng cách từ trọng tâm đến trung điểm của mỗi cạnh bằng ⅓ đường trung tuyến tương ứng với điểm đó.
- Tam giác đều: Trong tam giác đều, ba đường trung tuyến cũng đồng thời là đường cao, đường phân giác và đường trung trực.
Ứng Dụng Của Đường Trung Tuyến
Hiểu rõ “trung tuyến là j” và các tính chất của nó rất quan trọng trong giải toán hình học. Đường trung tuyến được sử dụng để:
- Tìm trọng tâm của tam giác, một điểm đặc biệt có nhiều ứng dụng trong cơ học và kỹ thuật.
- Chứng minh các bài toán liên quan đến tính đồng quy của các đường thẳng trong tam giác.
- Giải các bài toán về diện tích, vì đường trung tuyến chia tam giác thành hai tam giác có diện tích bằng nhau.
- Xác định các tính chất đặc biệt của tam giác, ví dụ như tam giác cân, tam giác đều.
Ví Dụ Minh Họa
Xét tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Tính độ dài đường trung tuyến ma ứng với cạnh BC.
Áp dụng công thức:
ma = √(2b² + 2c² - a²) / 2
= √(2(8²) + 2(6²) - (10²)) / 2
= √(128 + 72 - 100) / 2
= √100 / 2
= 10 / 2
= 5cmVậy độ dài đường trung tuyến ma là 5cm.
Hình ảnh minh họa giúp người đọc dễ dàng hình dung và áp dụng kiến thức về đường trung tuyến.
Kết Luận
Hy vọng bài viết này đã giúp bạn hiểu rõ câu hỏi “trung tuyến là j“, cũng như các công thức và tính chất liên quan đến đường trung tuyến. Đây là một khái niệm cơ bản nhưng quan trọng trong hình học, có nhiều ứng dụng trong giải toán và các lĩnh vực khác. Việc nắm vững kiến thức về đường trung tuyến sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán hình học phức tạp.