Khái Niệm Trọng Tâm Tứ Diện
Trong hình học không gian, Trọng Tâm Của Tứ Diện là một điểm đặc biệt, đóng vai trò quan trọng trong việc xác định các tính chất và mối liên hệ giữa các yếu tố của tứ diện đó. Để hiểu rõ hơn về trọng tâm tứ diện, chúng ta sẽ bắt đầu với bài toán cơ bản sau:
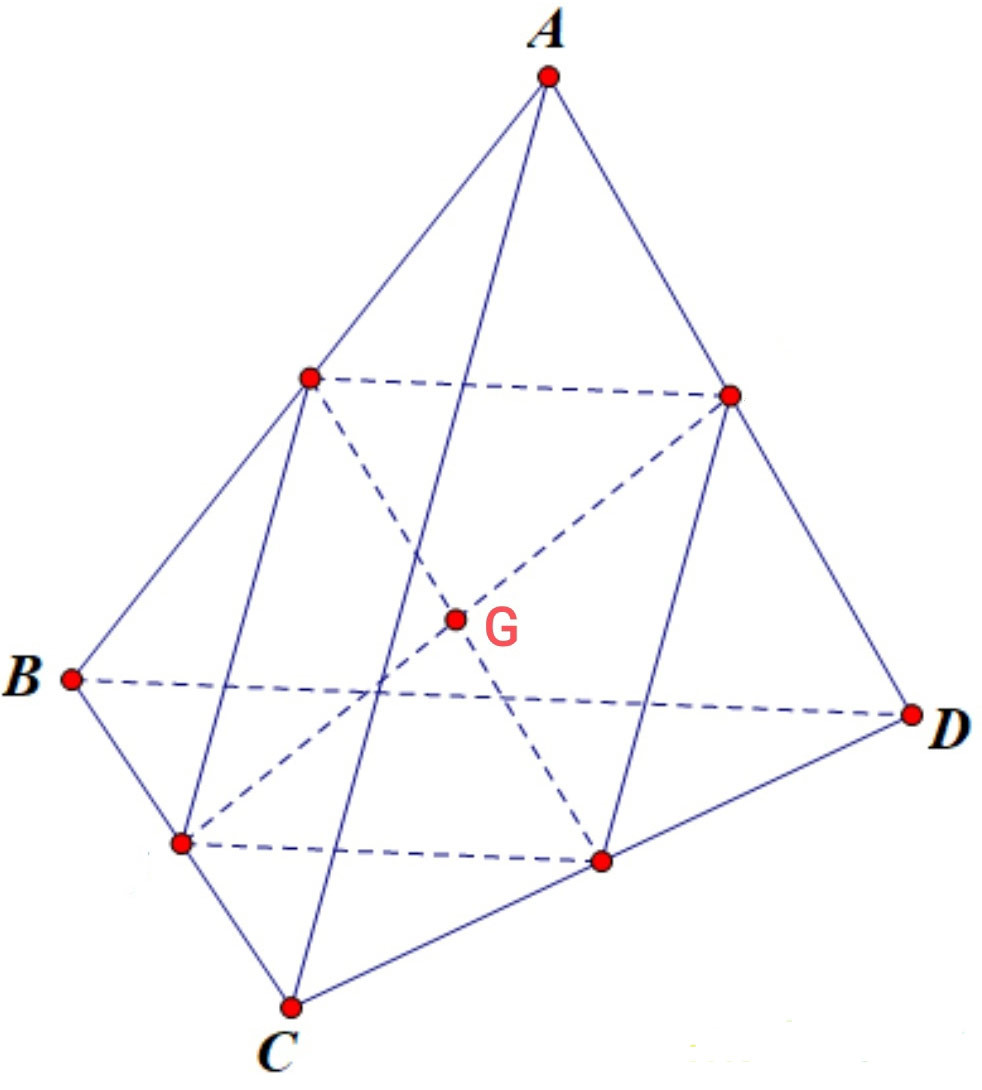
Bài toán: Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các đoạn thẳng AC, BD, AB, CD, AD, BC. Chứng minh rằng các đoạn thẳng MN, PQ, RS đồng quy tại trung điểm G của mỗi đoạn.
Điểm đồng quy G trong bài toán trên chính là trọng tâm của tứ diện ABCD. Như vậy, có thể định nghĩa:
Định nghĩa: Trọng tâm của một tứ diện là trung điểm của đoạn thẳng nối trung điểm của hai cạnh đối diện bất kỳ của tứ diện đó.
Tính Chất Quan Trọng Của Trọng Tâm Tứ Diện
Trọng tâm của tứ diện không chỉ là một điểm đơn thuần mà còn sở hữu những tính chất đặc biệt, giúp chúng ta giải quyết nhiều bài toán hình học không gian một cách hiệu quả.
Một trong những tính chất quan trọng nhất của trọng tâm G là:
$overrightarrow{GA} + overrightarrow{GB} + overrightarrow{GC} + overrightarrow{GD} = overrightarrow{0}$
Tính chất này thường được sử dụng để định nghĩa trọng tâm của tứ diện trong nhiều tài liệu tham khảo. Nó thể hiện sự cân bằng về mặt vectơ từ trọng tâm đến các đỉnh của tứ diện.
Chứng minh:
Để chứng minh tính chất trên, ta có thể sử dụng các quy tắc cộng vectơ và tính chất trung điểm. Gọi I là trung điểm của CD. Khi đó:
$overrightarrow{GA} + overrightarrow{GB} + overrightarrow{GC} + overrightarrow{GD} = (overrightarrow{GA} + overrightarrow{GB}) + (overrightarrow{GC} + overrightarrow{GD}) = 2overrightarrow{GI} + 2overrightarrow{GJ}$
Với J là trung điểm của AB. Vì G là trung điểm của IJ nên $overrightarrow{GI} + overrightarrow{GJ} = overrightarrow{0}$. Suy ra điều phải chứng minh.
Ứng Dụng của Trọng Tâm Tứ Diện trong Giải Toán
Để hiểu rõ hơn về cách áp dụng các kiến thức về trọng tâm tứ diện vào giải toán, chúng ta sẽ xét một ví dụ cụ thể.
Bài tập: Cho tứ diện ABCD. Gọi G là trọng tâm của tứ diện. Chứng minh rằng: $overrightarrow{OG} = frac{1}{4}(overrightarrow{OA} + overrightarrow{OB} + overrightarrow{OC} + overrightarrow{OD})$ với O là một điểm bất kỳ trong không gian.
Giải:
Xuất phát từ tính chất $overrightarrow{GA} + overrightarrow{GB} + overrightarrow{GC} + overrightarrow{GD} = overrightarrow{0}$, ta chèn điểm O vào mỗi vectơ:
$(overrightarrow{OA} – overrightarrow{OG}) + (overrightarrow{OB} – overrightarrow{OG}) + (overrightarrow{OC} – overrightarrow{OG}) + (overrightarrow{OD} – overrightarrow{OG}) = overrightarrow{0}$
Suy ra: $overrightarrow{OA} + overrightarrow{OB} + overrightarrow{OC} + overrightarrow{OD} = 4overrightarrow{OG}$
Vậy: $overrightarrow{OG} = frac{1}{4}(overrightarrow{OA} + overrightarrow{OB} + overrightarrow{OC} + overrightarrow{OD})$ (điều phải chứng minh).
Qua bài tập trên, chúng ta thấy rằng trọng tâm của tứ diện có thể được xác định thông qua trung bình cộng các vectơ từ một điểm bất kỳ đến các đỉnh của tứ diện.