Trong Một Cuộc Thi Pha Chế, việc tối ưu hóa nguyên liệu để đạt được điểm thưởng cao nhất là yếu tố then chốt dẫn đến thành công. Một bài toán điển hình đặt ra là làm thế nào để pha chế nước cam và nước táo với số lượng bao nhiêu, khi nguồn lực (hương liệu, nước, đường) có hạn?
Giả sử, mỗi đội chơi có tối đa 24g hương liệu, 9 lít nước và 210g đường. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu. Tương tự, 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Biết rằng, mỗi lít nước cam mang lại 60 điểm thưởng, mỗi lít nước táo mang lại 80 điểm thưởng. Câu hỏi đặt ra là: Cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
Để giải quyết bài toán này, chúng ta cần thiết lập một hệ phương trình và bất phương trình, sau đó tìm ra nghiệm tối ưu. Gọi x là số lít nước cam và y là số lít nước táo cần pha chế. Ta có các điều kiện ràng buộc sau:
- Lượng đường: 30x + 10y ≤ 210
- Lượng nước: x + y ≤ 9
- Lượng hương liệu: x + 4y ≤ 24
- Điều kiện không âm: x ≥ 0, y ≥ 0
Mục tiêu là tối đa hóa hàm mục tiêu (điểm thưởng): P(x; y) = 60x + 80y.
Để giải bài toán này, chúng ta có thể sử dụng phương pháp đồ thị để tìm ra miền nghiệm, sau đó xác định các điểm cực trị (giao điểm của các đường thẳng trong hệ bất phương trình). Giá trị lớn nhất của hàm mục tiêu P(x; y) tại một trong các điểm cực trị sẽ là đáp án.
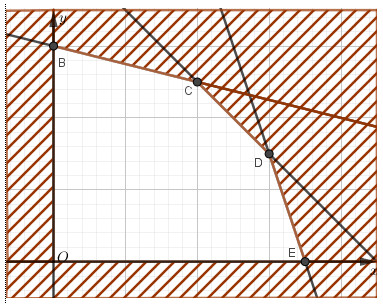Miền nghiệm bài toán pha chế nước cam táo, thể hiện vùng khả thi và các điểm cực trị để tối ưu hóa điểm thưởng trong cuộc thi pha chế.
Miền nghiệm được biểu diễn trên đồ thị là một đa giác, và các đỉnh của đa giác này chính là các điểm cực trị. Việc thay tọa độ các điểm cực trị vào hàm P(x; y) sẽ cho ta biết giá trị lớn nhất của điểm thưởng.
Ví dụ, sau khi vẽ đồ thị và xác định các đỉnh của miền nghiệm, ta có thể có các điểm như O(0;0), B(0;6), C(4;5), D(6;3), E(7;0). Thay các giá trị này vào P(x; y) = 60x + 80y, ta được:
- P(0;0) = 0
- P(0;6) = 480
- P(4;5) = 640
- P(6;3) = 600
- P(7;0) = 420
Từ đó, ta thấy P(4;5) = 640 là giá trị lớn nhất. Vậy, để đạt được số điểm thưởng cao nhất, đội chơi cần pha chế 4 lít nước cam và 5 lít nước táo.
Bài toán này không chỉ là một ví dụ về ứng dụng toán học trong thực tế mà còn thể hiện tầm quan trọng của việc tối ưu hóa nguồn lực trong một cuộc thi pha chế. Việc phân tích và giải quyết bài toán một cách hiệu quả sẽ giúp các đội chơi đưa ra quyết định chính xác và đạt được kết quả tốt nhất.
