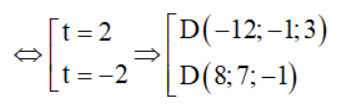Trong hình học không gian, việc sử dụng hệ tọa độ Oxyz là một công cụ mạnh mẽ giúp giải quyết nhiều bài toán phức tạp. Nó cho phép chúng ta biểu diễn các điểm, đường thẳng, mặt phẳng và các hình khối bằng các phương trình và tọa độ số, từ đó áp dụng các phương pháp đại số để tìm ra lời giải. Dưới đây là một số ví dụ minh họa về cách sử dụng hệ tọa độ Oxyz để giải các bài toán hình học không gian thường gặp.
Câu 1
Cho ba điểm A(1;0;0), B(0;0;1), C(2;1;0) trong không gian với hệ tọa độ Oxyz. Chứng minh A, B, C tạo thành một tam giác và tính diện tích tam giác ABC.
Bài giải:
Ta có: $overline{AB}= (-1; 0; 1) ;overline{AC}= (1; 1; 0)$
Suy ra: Hai vectơ $overrightarrow{AB}$ và $overrightarrow{AC}$ không cùng phương.
Vậy A, B, C không thẳng hàng, do đó ABC tạo thành một tam giác.
Diện tích tam giác ABC là:
$S_{ABC}=frac{1}{2}left | left [ overline{AB};overline{AC} right ] right |=frac{1}{2}.sqrt{(-1)^{2}+1^{2}+(-1)^{2}}=frac{sqrt{3}}{2}$
Vậy A, B, C tạo thành một tam giác có diện tích là $frac{sqrt{3}}{2}$.
Câu 2
Cho 3 điểm A(2;-3;7), B(0;4;-3) và C(4;2;5) trong không gian với hệ trục tọa độ Oxyz. Tìm tọa độ của điểm M trên mặt phẳng (Oxy) sao cho |MA +MB + MC| có giá trị nhỏ nhất?
Bài giải:
Theo bài ra ta có:
$left | overline{MA}+overline{MB}+overline{MC} right | =left | overline{MG}+overline{GA}+overline{MG}+overline{GB}+overline{MG}+overline{GC} right |=left | 3overline{MG}+overline{GA}+overline{GB}+overline{GC} right |$
Đầu tiên ta xác định tọa độ điểm G sao cho: $overline{GA}+overline{GB}+overline{GC}=overline{0}$
hay nói cách khác G là trọng tâm tam giác ABC. Ta có:
G = $left (frac{0+2+4}{3};frac{-3+4+2}{3};frac{7-3+5}{3} right )$ => Tọa độ điểm G (2; 1; 3)
Từ đó: $left | overline{MA}+overline{MB}+overline{MC} right | = left | 3overline{MG} right | = 3.MG$
$left | overline{MA}+overline{MB}+overline{MC} right |$ nhỏ nhất khi và chỉ khi MG nhỏ nhất. Mà M nằm trên mặt phẳng (Oxy) nên M là hình chiếu của G lên (Oxy)
=> M(2;1;0)
Vậy tọa độ điểm M(2;1;0) thì $left | overline{MA}+overline{MB}+overline{MC} right |$ có giá trị nhỏ nhất.
Câu 3:
Cho ba điểm A(1;0;1), B(1;2;1), C(4;1;-2) trong không gian với hệ tọa độ Oxyz, và mặt phẳng P : x + y + z = 0. Trong các điểm (1;1;-1), (1;1;1) , (1;2;-1) , (1;0;-1), điểm nào là điểm M trên (P) thỏa mãn $MA^{2}+MB^{2}+MC^{2}$ đạt giá trị nhỏ nhất?
Bài giải:
Gọi G là trọng tâm tam giác ABC. Ta có:
G=$left ( frac{1+1+4}{3};frac{0+2+1}{3};frac{1+1-2}{3}right )$ => G(2;1;0)
T = $MA^{2}+MB^{2}+MC^{2}$
T = $(overline{MG}+overline{GA})^{2}+(overline{MG}+overline{GB})^{2}+(overline{MG}+overline{GC})^{2}$
T = $3MG^{2}+GA^{2}+GB^{2}+GC^{2}+2overline{MG}(overline{MA}+overline{MB}+overline{MC})$
T = $3MG^{2}+GA^{2}+GB^{2}+GC^{2}+2overline{MG}.overline{0}$
T = $3MG^{2}+GA^{2}+GB^{2}+GC^{2}$
Do $GA^{2}+GB^{2}+GC^{2}$ cố định nên $T_{min}$ khi $MG_{min}$.
=> Mà M thuộc (P) nên M là hình chiếu vuông góc của G lên (P)
Gọi (d) là đường thẳng qua G và vuông góc (P) => Phương trình đường thẳng d là:
M là giao điểm của d và (P) nên thỏa mãn: 2 + t +1 + t +t = 0 ⇔ t = -1
=> M (1; 0; -1)
Câu 4
Cho ba điểm A(-2;3;1), B(2;1;0) và C(-3;-1;1) trong không gian với hệ tọa độ Oxyz. Tìm điểm D sao cho ABCD là hình thang có đáy AD và $S_{ABCD}=3S_{Delta ABC}$.
Bài giải:
Vì tứ giác ABCD là hình thang
=> AD//BC => $overline{u}_{AD} = overline{u}_{BC} = (-5; -2; 1)$
=> Phương trình đường thẳng AD là :
=$frac{x+2}{-5}=frac{y-3}{-2}=frac{z-1}{1}$
=> D(-5t – 2; -2t + 3; t + 1)
Ta có:
$S_{ABCD}$ = 3S_{ABCD} ⇔ S_{ABC} + S_{ACD} = 3S_{ABC}$
⇔ $S_{ACD} = 2S_{ABC}$
Mà diện tích tam giác ABC là:
$S_{ABC} = =frac{1}{2}left | left [ overline{AB}; overline{AC}right ] right |=frac{sqrt{341}}{2} => S_{ACD}=sqrt{341}$
Hay nói cách khác:
$S_{ACD} = frac{1}{2}left | left [ overline{AD};overline{AC} right ] right |=sqrt{341}$
=> $frac{1}{2}sqrt{341t^{2}}=sqrt{341}$
Do ABCD là hình thang => D(-12; -1; 3)
Câu 5
Cho ba điểm A(1;1;1), B(0;1;2), C(-2;1;4) trong không gian với hệ tọa độ Oxyz và mặt phẳng (P): x-y+z+2=0. Biết điểm N ∊ (P). Trong các điểm (-2;0;1), $(frac{4}{3}; 3;frac{3}{2})$, $(frac{1}{2}; 2; 1)$, (-1; 2;1), điểm nào là tọa độ điểm N sao cho S = $2NA^{2}+NB^{2} + NC^{2}$ đạt giá trị nhỏ nhất.
Bài giải:
Gọi M(a; b; c) thỏa mãn đẳng thức vectơ $2overline{MA}+overline{MB}+overline{MC} = 0$
⇔ 2(1-a;1-b;1-c) + (0-a; 1-b; 2-c) + (-2-a; 1-b; 4-c) = 0
⇔ (-4a;4-4b;8-4c) = 0
Khi đó:
S = $2NA^{2}+NB^{2}+NC^{2}=2overline{NA}^{2}+overline{NB}^{2}+overline{NC}^{2}$
= $2left ( overline{MN}+overline{MA} right )^{2}+left ( overline{MN}+overline{MB} right )^{2}+left ( overline{MN}+overline{MC} right )^{2}= 4MN2 + 2NM.(2MA +MB + MC ) + 2MA2+MB2 + MC2$
= $4MN^{2}+2MA^{2}+MB^{2}+MC^{2} (do 2overline{MA}+overline{MB}+overline{MC}=overline{0})$
Vì $2MA^{2}+MB^{2}+MC^{2}$ = const suy ra $S_{min}$ ⇔ $MN_{min}$
⇔ N là hình chiếu của M trên (P) => MN ⊥ (P)
Phương trình đường thẳng MN là:
$frac{x}{1}=frac{y-1}{-1}=frac{z-2}{1}$ => N(t; 1 – t; t + 2)
mà $N in (P)$ suy ra: t – (1 – t) + t + 2 + 2 =0
⇔ t = -1 => N (-1;2;1)
Kết luận:
Thông qua các ví dụ trên, ta thấy rằng việc áp dụng hệ tọa độ Oxyz giúp chúng ta chuyển đổi các bài toán hình học không gian thành các bài toán đại số, từ đó dễ dàng giải quyết bằng các công cụ toán học. Nắm vững kiến thức về hệ tọa độ Oxyz là rất quan trọng để học tốt môn Toán hình học không gian.