Dao động điều hòa là một hiện tượng vật lý quan trọng, xuất hiện phổ biến trong tự nhiên và kỹ thuật. Hiểu rõ về dao động điều hòa giúp chúng ta giải thích và ứng dụng nhiều hiện tượng xung quanh, từ chuyển động của con lắc đến hoạt động của các mạch điện tử.
1. Khái Niệm Dao Động Điều Hòa
1.1. Dao Động Cơ
Dao động cơ là chuyển động qua lại của một vật quanh một vị trí cân bằng. Ví dụ, một chiếc lá rung trên cành cây là một dạng dao động cơ.
1.2. Định Nghĩa Dao Động Điều Hòa
Dao động điều hòa là một dạng dao động cơ đặc biệt, trong đó li độ của vật biến thiên theo hàm sin hoặc cosin của thời gian. Điều này có nghĩa là vật chuyển động qua lại quanh vị trí cân bằng theo một quy luật nhất định, lặp đi lặp lại theo thời gian.
Ví dụ về dao động điều hòa:
- Chuyển động của quả lắc đồng hồ (trong điều kiện lý tưởng).
- Sự rung động của một sợi dây đàn guitar sau khi gảy.
- Chuyển động của một vật gắn vào lò xo khi kéo ra khỏi vị trí cân bằng và thả ra.
Dao động điều hòa có quỹ đạo là một đoạn thẳng, và li độ của vật được mô tả bằng hàm cosin hoặc sin theo thời gian. Chính vì vậy, đồ thị của dao động điều hòa có dạng hình sin.
Hình ảnh trên minh họa đồ thị hình sin của dao động điều hòa, thể hiện rõ sự biến thiên tuần hoàn của li độ theo thời gian.
1.3. Phương Trình Dao Động Điều Hòa
Phương trình dao động điều hòa có dạng tổng quát như sau:
x = Acos(ωt + φ)
Trong đó:
- x: Li độ của vật tại thời điểm t.
- A: Biên độ dao động (khoảng cách lớn nhất từ vị trí cân bằng).
- ω: Tần số góc của dao động (đo bằng rad/s).
- t: Thời gian (đo bằng giây).
- (ωt + φ): Pha dao động tại thời điểm t (đo bằng radian).
- φ: Pha ban đầu của dao động (đo bằng radian), cho biết trạng thái ban đầu của vật.
Cách xác định các đại lượng:
-
Biên độ A:
-
Tần số góc ω:
-
Pha ban đầu φ:
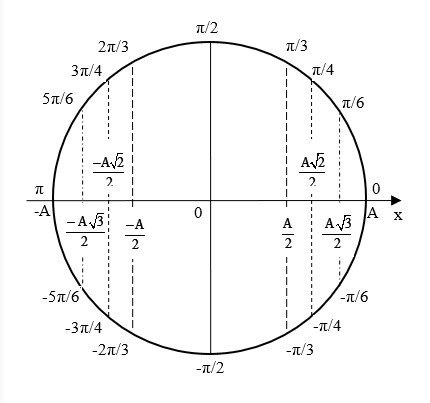
Hình ảnh vòng tròn lượng giác giúp xác định pha ban đầu của dao động điều hòa một cách trực quan.
2. Các Đại Lượng Đặc Trưng Trong Dao Động Điều Hòa
Hiểu rõ các đại lượng đặc trưng này là chìa khóa để giải quyết các bài toán liên quan đến dao động điều hòa.
2.1. Chu Kỳ (T)
Chu kỳ là khoảng thời gian ngắn nhất để vật thực hiện một dao động toàn phần. Đơn vị của chu kỳ là giây (s).
Công thức liên hệ giữa chu kỳ và tần số góc:
T = 2π/ω
2.2. Tần Số (f)
Tần số là số dao động toàn phần mà vật thực hiện được trong một giây. Đơn vị của tần số là Hertz (Hz).
Công thức liên hệ giữa tần số và chu kỳ:
f = 1/T
Công thức liên hệ giữa tần số và tần số góc:
f = ω/2π
2.3. Tần Số Góc (ω)
Tần số góc là đại lượng đặc trưng cho tốc độ biến thiên của pha dao động.
Công thức liên hệ giữa tần số góc, chu kỳ và tần số:
ω = 2π/T = 2πf
2.4. Vận Tốc (v)
Vận tốc của vật Trong Dao động điều Hòa biến thiên theo thời gian và đạt giá trị cực đại tại vị trí cân bằng.
Công thức tính vận tốc:
v = -Aωsin(ωt + φ)
Vận tốc cực đại:
vmax = ωA
Vận tốc đổi chiều tại vị trí biên và nhanh pha hơn li độ một góc π/2.
2.5. Gia Tốc (a)
Gia tốc của vật trong dao động điều hòa cũng biến thiên theo thời gian và đạt giá trị cực đại tại vị trí biên.
Công thức tính gia tốc:
a = -ω²x = -Aω²cos(ωt + φ)
Gia tốc cực đại:
amax = ω²A
Gia tốc ngược pha với li độ và sớm pha hơn vận tốc một góc π/2.
3. Đồ Thị Dao Động Điều Hòa
Đồ thị của dao động điều hòa là một đường hình sin, thể hiện sự biến thiên của li độ theo thời gian. Hình dạng của đồ thị phụ thuộc vào pha ban đầu φ.
Hình ảnh trên biểu diễn đồ thị dao động điều hòa khi pha ban đầu bằng 0, bắt đầu từ biên độ cực đại.
Hình ảnh trên cho thấy các dạng đồ thị khác nhau tùy thuộc vào giá trị của pha ban đầu.
4. Các Dạng Bài Tập Dao Động Điều Hòa Thường Gặp
Việc luyện tập giải các dạng bài tập khác nhau giúp củng cố kiến thức và kỹ năng giải quyết vấn đề liên quan đến dao động điều hòa.
4.1. Bài Tập Tìm Các Đại Lượng Đặc Trưng
Dạng bài này yêu cầu xác định các đại lượng như biên độ, tần số, chu kỳ, pha ban đầu, vận tốc, gia tốc dựa trên thông tin đề bài cung cấp.
Ví dụ:
Một vật dao động điều hòa theo trục Ox có đồ thị như hình vẽ. Tính tần số góc của dao động.
Giải:
Dựa vào đồ thị, ta thấy khoảng thời gian giữa hai lần liên tiếp li độ x = 0 là T/2 = 0.2 s => T = 0.4 s.
Vậy, tần số góc là: ω = 2π/T = 5π (rad/s).
4.2. Bài Tập Tìm Quãng Đường Trong Một Khoảng Thời Gian
Dạng bài này yêu cầu tính quãng đường vật đi được trong một khoảng thời gian nhất định.
Các bước giải:
- Xác định trạng thái ban đầu của vật (li độ, vận tốc).
- Phân tích khoảng thời gian Δt.
- Sử dụng mối liên hệ giữa dao động điều hòa và chuyển động tròn đều để tính quãng đường.
4.3. Bài Tập Tìm Quãng Đường Ngắn Nhất, Dài Nhất
Dạng bài này yêu cầu tìm quãng đường lớn nhất hoặc nhỏ nhất mà vật đi được trong một khoảng thời gian cho trước.
4.4. Bài Tập Tính Tốc Độ Trung Bình, Vận Tốc Trung Bình
Dạng bài này yêu cầu tính tốc độ trung bình và vận tốc trung bình của vật trong một khoảng thời gian nhất định.
Công thức:
- Tốc độ trung bình: vtb = S/Δt
- Vận tốc trung bình: (tổng các quãng đường theo hướng)/Δt
Kết luận:
Dao động điều hòa là một chủ đề quan trọng trong chương trình Vật lý phổ thông. Việc nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập là yếu tố then chốt để đạt điểm cao trong các kỳ thi.