1. Định Nghĩa Tổng Hai Vecto
Trong hình học, tổng của hai vecto là một khái niệm cơ bản. Cho hai vecto (overrightarrow{a}) và (overrightarrow{b}). Để xác định tổng của chúng, ta chọn một điểm (A) bất kỳ. Từ (A), ta vẽ vecto (overrightarrow{AB}) bằng (overrightarrow{a}) và từ (B) vẽ vecto (overrightarrow{BC}) bằng (overrightarrow{b}). Khi đó, vecto (overrightarrow{AC}) chính là tổng của hai vecto (overrightarrow{a}) và (overrightarrow{b}).
Ký hiệu: (overrightarrow{AC}) = (overrightarrow{a}) + (overrightarrow{b}).
2. Quy Tắc Hình Bình Hành trong Tổng Hai Vecto
Một trường hợp đặc biệt và quan trọng khác để xác định tổng hai vecto là quy tắc hình bình hành. Nếu chúng ta có một hình bình hành (ABCD), thì tổng của hai vecto (overrightarrow{AB}) và (overrightarrow{AD}) sẽ bằng vecto (overrightarrow{AC}), là đường chéo của hình bình hành đó.
(overrightarrow{AB}) + (overrightarrow{AD}) = (overrightarrow{AC}).
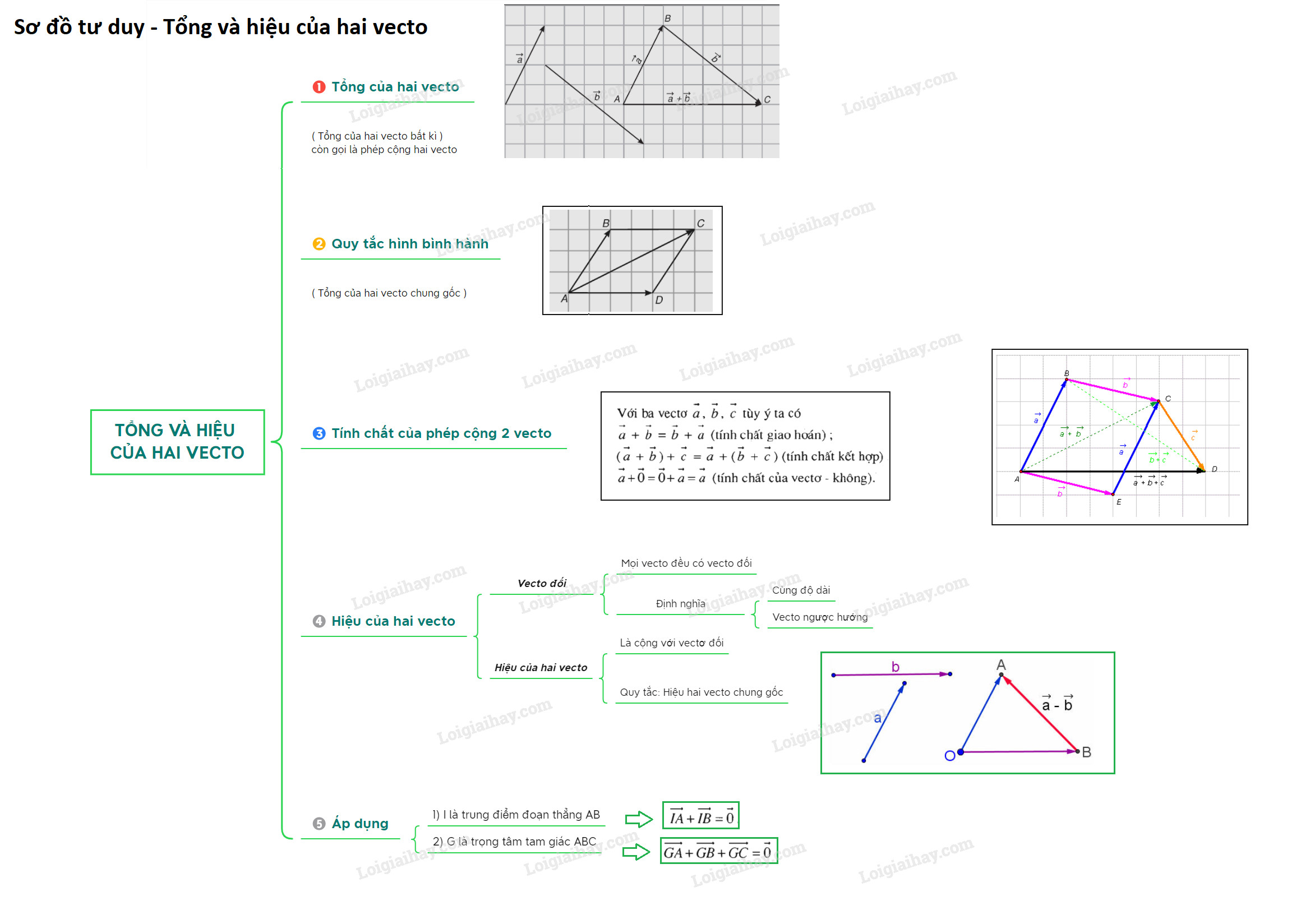Hình bình hành ABCD minh họa quy tắc tổng hai vecto, với AC là đường chéo thể hiện tổng của AB và AD.
3. Các Tính Chất Quan Trọng của Tổng Hai Vecto
Tổng của hai vecto sở hữu nhiều tính chất quan trọng, giúp đơn giản hóa các phép toán và chứng minh trong hình học:
-
Tính chất giao hoán: Thứ tự cộng không ảnh hưởng đến kết quả.
(overrightarrow{a}) + (overrightarrow{b}) = (overrightarrow{b}) + (overrightarrow{a}) -
Tính chất kết hợp: Khi cộng ba vecto trở lên, ta có thể nhóm chúng theo bất kỳ thứ tự nào.
((overrightarrow{a}) + (overrightarrow{b}) ) + (overrightarrow{c}) = (overrightarrow{a}) + ((overrightarrow{b}) +(overrightarrow{c})) -
Tính chất của vecto không: Vecto không cộng với bất kỳ vecto nào cũng bằng chính vecto đó.
(overrightarrow{a})+(overrightarrow{0}) = (overrightarrow{0}) + (overrightarrow{a}) (=overrightarrow{a})
4. Vecto Đối và Hiệu của Hai Vecto
-
Vecto đối: Vecto đối của vecto (overrightarrow{a}), ký hiệu (-overrightarrow{a}), là vecto có cùng độ dài nhưng ngược hướng với (overrightarrow{a}). Vecto đối của (overrightarrow{0}) là chính nó.
-
Hiệu của hai vecto: Hiệu của hai vecto (overrightarrow{a}) và (overrightarrow{b}), ký hiệu (overrightarrow{a})- (overrightarrow{b}), được định nghĩa là tổng của (overrightarrow{a}) và vecto đối của (overrightarrow{b}):
(overrightarrow{a})- (overrightarrow{b}) = (overrightarrow{a}) + (-(overrightarrow{b})).
5. Ứng Dụng của Tổng Hai Vecto
Tổng hai vecto có nhiều ứng dụng trong hình học và vật lý:
-
Trung điểm của đoạn thẳng: Điểm (I) là trung điểm của đoạn thẳng (AB) khi và chỉ khi tổng hai vecto (overrightarrow{IA}) và (overrightarrow{IB}) bằng vecto không.
(overrightarrow{IA}) +(overrightarrow{IB}) = (overrightarrow{0})
-
Trọng tâm của tam giác: Điểm (G) là trọng tâm của tam giác (ABC) khi và chỉ khi tổng ba vecto (overrightarrow{GA}), (overrightarrow{GB}) và (overrightarrow{GC}) bằng vecto không.
(overrightarrow{GA}) + (overrightarrow{GB})+(overrightarrow{GC}) = (overrightarrow{0})
Việc nắm vững định nghĩa, tính chất và các ứng dụng của tổng hai vecto là nền tảng quan trọng để học tốt hình học vecto và các môn khoa học liên quan.
