Hình tứ giác là một hình học cơ bản và quan trọng. Hiểu rõ về hình tứ giác giúp học sinh giải quyết các bài toán hình học hiệu quả hơn. Bài viết này sẽ cung cấp kiến thức đầy đủ về “Tổng 4 Góc Tứ Giác”, các loại tứ giác và bài tập vận dụng.
Định Nghĩa và Tính Chất Cơ Bản Của Tứ Giác
Tứ giác là một đa giác có bốn đỉnh và bốn cạnh, trong đó không có bất kỳ hai cạnh nào cùng nằm trên một đường thẳng. Tứ giác có thể là tứ giác lồi hoặc tứ giác lõm.
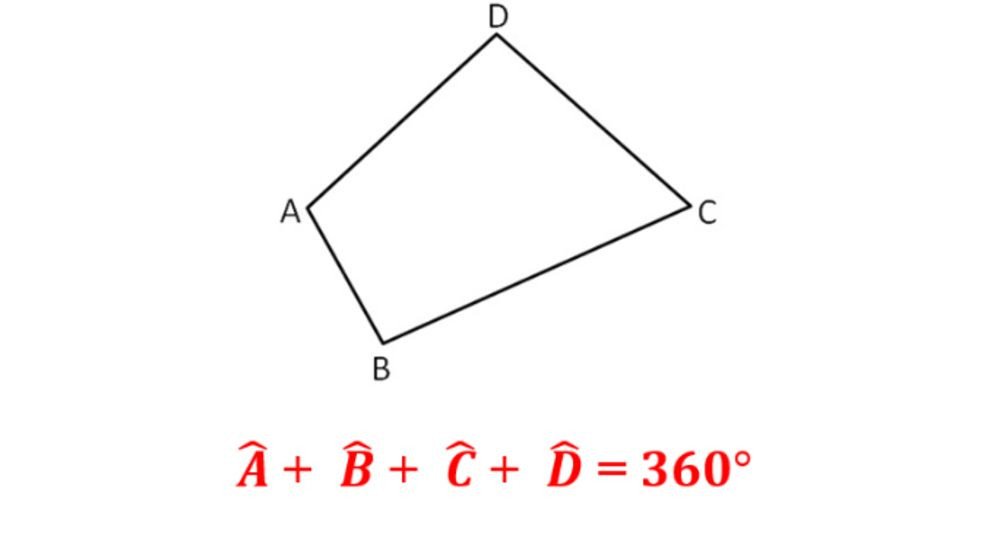
Định lý quan trọng: Tổng các góc trong một tứ giác luôn bằng 360 độ.
∠A + ∠B + ∠C + ∠D = 360°
Hình ảnh minh họa tứ giác ABCD với các góc A, B, C, D, thể hiện rõ các đỉnh và cạnh của hình.
Tính chất hình chéo của tứ giác: Hai đường chéo của một tứ giác lồi giao nhau tại một điểm thuộc miền trong của tứ giác. Nếu tứ giác có hai đường chéo giao nhau tại một điểm thuộc miền trong của nó thì đó là tứ giác lồi.
Phân Loại Tứ Giác
Tứ giác có thể được phân loại thành nhiều loại khác nhau, dựa trên các đặc điểm về cạnh và góc:
- Tứ giác lồi: Tứ giác có 4 góc đều nhỏ hơn 180 độ và hai đường chéo nằm bên trong hình.
Hình ảnh minh họa một tứ giác lồi, trong đó tất cả các góc đều nhỏ hơn 180 độ và hai đường chéo nằm hoàn toàn bên trong hình.
- Tứ giác lõm: Tứ giác chứa một góc có số đo lớn hơn 180 độ và một trong hai đường chéo nằm bên ngoài tứ giác.
- Tứ giác không đều: Tứ giác không có cặp cạnh nào song song với nhau.
Các Dạng Tứ Giác Đặc Biệt
Ngoài các loại tứ giác cơ bản, còn có một số dạng tứ giác đặc biệt với những tính chất riêng:
- Hình thang: Tứ giác có ít nhất hai cạnh đối song song.
Hình ảnh minh họa hình thang, nhấn mạnh hai cạnh đáy song song và các yếu tố cấu thành hình thang.
- Hình thang cân: Hình thang có hai góc kề một cạnh đáy bằng nhau.
- Hình bình hành: Tứ giác có hai cặp cạnh đối song song.
Hình ảnh minh họa hình bình hành, thể hiện rõ các cạnh đối song song và bằng nhau, cũng như các góc đối bằng nhau.
- Hình thoi: Tứ giác có bốn cạnh bằng nhau.
Hình ảnh minh họa hình thoi, làm nổi bật bốn cạnh bằng nhau và tính chất của đường chéo.
- Hình chữ nhật: Tứ giác có bốn góc vuông.
Hình ảnh minh họa hình chữ nhật, nhấn mạnh bốn góc vuông và tính chất của các cạnh đối.
- Hình vuông: Tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Hình ảnh minh họa hình vuông, thể hiện rõ bốn góc vuông và bốn cạnh bằng nhau, cũng như tính chất đặc biệt của đường chéo.
- Tứ giác nội tiếp: Tứ giác có bốn đỉnh nằm trên cùng một đường tròn.
Hình ảnh minh họa tứ giác nội tiếp, các đỉnh của tứ giác nằm trên đường tròn, giúp hình dung rõ ràng khái niệm.
Các Công Thức Tính Chu Vi và Diện Tích Tứ Giác
- Chu vi tứ giác: P = a + b + c + d (a, b, c, d là độ dài các cạnh).
- Diện tích tứ giác: Công thức tính diện tích phụ thuộc vào từng loại tứ giác cụ thể.
Bài Tập Vận Dụng
Bài 1: Cho tứ giác ABCD có ∠A = 70°, ∠B = 110°, ∠C = 80°. Tính ∠D.
Giải:
Áp dụng định lý tổng 4 góc tứ giác:
∠A + ∠B + ∠C + ∠D = 360°
70° + 110° + 80° + ∠D = 360°
260° + ∠D = 360°
∠D = 360° – 260° = 100°
Vậy ∠D = 100°.
Bài 2: Tứ giác EFGH có phải là hình bình hành không, nếu ∠E = 60°, ∠F = 120°, ∠G = 60°? Giải thích.
Giải:
Nếu EFGH là hình bình hành thì ∠E = ∠G và ∠F = ∠H. Tổng các góc trong tứ giác là 360°.
∠H = 360° – (∠E + ∠F + ∠G) = 360° – (60° + 120° + 60°) = 120°
Vì ∠F = ∠H = 120°, nên tứ giác EFGH có thể là hình bình hành. Cần thêm thông tin về cạnh để khẳng định chắc chắn.
Bài 3: Tính tổng các góc ngoài của một tứ giác.
Giải:
Tổng các góc ngoài của một tứ giác luôn bằng 360 độ. Điều này có thể chứng minh bằng cách sử dụng tính chất góc ngoài và tổng các góc trong của tứ giác.
Bí Quyết Ghi Nhớ Kiến Thức Về Hình Tứ Giác
- Nắm vững lý thuyết cơ bản: Đảm bảo hiểu rõ định nghĩa, tính chất và phân loại các loại tứ giác.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng toán và áp dụng kiến thức.
- Sử dụng hình ảnh minh họa: Vẽ hình và sử dụng các công cụ trực quan để dễ dàng hình dung và ghi nhớ.
- Học nhóm: Trao đổi và thảo luận với bạn bè để hiểu sâu hơn về các khái niệm và phương pháp giải toán.
Nắm vững kiến thức về “tổng 4 góc tứ giác” và các dạng bài tập liên quan sẽ giúp học sinh tự tin hơn trong môn Hình học và đạt kết quả tốt hơn trong học tập.