Tọa Độ Tâm Đối Xứng của Đồ Thị Hàm Số: Lý Thuyết, Ví Dụ và Ứng Dụng

Trong thế giới toán học, đặc biệt là hình học giải tích, việc xác định Tọa độ Tâm đối Xứng Của đồ Thị Hàm Số là một kỹ năng vô cùng quan trọng. Nó không chỉ giúp ta hiểu sâu sắc hơn về tính chất đối xứng của hàm số mà còn mở ra cánh cửa ứng dụng vào nhiều lĩnh vực thực tế. Bài viết này sẽ đi sâu vào khái niệm, phương pháp xác định và những ứng dụng thú vị của tâm đối xứng trong đồ thị hàm số.

1. Định Nghĩa Tâm Đối Xứng của Đồ Thị Hàm Số

Tâm đối xứng của một đồ thị hàm số là một điểm đặc biệt, mà nếu ta lấy đối xứng bất kỳ điểm nào trên đồ thị qua điểm này, điểm đối xứng đó cũng sẽ thuộc đồ thị. Nói một cách hình học, đồ thị hàm số “cân bằng” xung quanh điểm này.

Về mặt toán học, điểm I(a, b) là tâm đối xứng của đồ thị hàm số y = f(x) nếu và chỉ nếu với mọi x, ta có:

f(x + a) + f(-x + a) = 2b

Công thức này thể hiện rằng giá trị của hàm số tại điểm cách a một đoạn x, cộng với giá trị của hàm số tại điểm cách a một đoạn -x, luôn bằng 2 lần giá trị b (tọa độ y của tâm đối xứng).

2. Tính Chất Quan Trọng Liên Quan Đến Tâm Đối Xứng

• Hàm số lẻ: Một hàm số được gọi là hàm số lẻ nếu f(-x) = -f(x) với mọi x thuộc tập xác định. Điểm đặc biệt là, đồ thị của hàm số lẻ luôn nhận gốc tọa độ O(0, 0) làm tâm đối xứng.

• Hàm số bậc ba: Hàm số bậc ba có dạng y = ax³ + bx² + cx + d (với a ≠ 0). Đồ thị của hàm số bậc ba luôn có tâm đối xứng, và tâm đối xứng này chính là điểm uốn của đồ thị. Điểm uốn là điểm mà tại đó đồ thị chuyển từ trạng thái lồi sang lõm, hoặc ngược lại. Việc tìm điểm uốn sẽ giúp ta dễ dàng xác định tọa độ tâm đối xứng.

3. Phương Pháp Xác Định Tọa Độ Tâm Đối Xứng: Chi Tiết Từng Bước

Để tìm tọa độ tâm đối xứng của đồ thị hàm số, ta có thể áp dụng phương pháp sau:

Bước 1: Giả sử tâm đối xứng.

Giả sử đồ thị hàm số y = f(x) có tâm đối xứng là điểm I(a, b).

Bước 2: Thực hiện phép tịnh tiến hệ tọa độ.

Thực hiện phép tịnh tiến hệ tọa độ Oxy sang hệ tọa độ IXY theo công thức:

x = X + a
y = Y + b

Phép tịnh tiến này giúp ta chuyển hệ quy chiếu, đưa điểm I(a, b) về gốc tọa độ của hệ tọa độ mới.

Bước 3: Viết lại phương trình hàm số trong hệ tọa độ mới.

Thay x = X + a và y = Y + b vào phương trình y = f(x) để được phương trình mới:

Y + b = f(X + a)

Từ đó, rút ra phương trình Y = f(X + a) – b.

Bước 4: Sử dụng tính chất đối xứng để tìm a và b.

Để I(a, b) là tâm đối xứng, hàm số Y = f(X + a) – b phải là hàm số lẻ đối với biến X. Điều này có nghĩa là:

f(-X + a) - b = -[f(X + a) - b]

Từ phương trình này, ta sẽ tìm ra các giá trị của a và b.

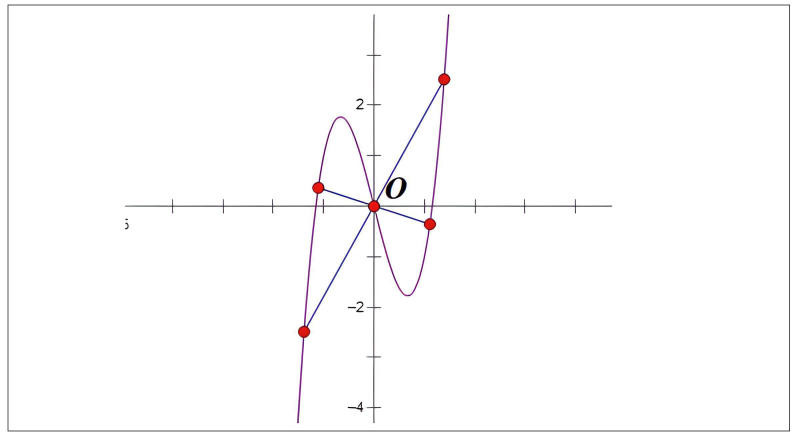Phương Pháp Xác Định Tâm Đối Xứng

Hình ảnh minh họa các bước xác định tọa độ tâm đối xứng của đồ thị hàm số bằng phép tịnh tiến hệ trục tọa độ.

4. Ví Dụ Minh Họa Chi Tiết

Để hiểu rõ hơn về phương pháp xác định tọa độ tâm đối xứng, hãy cùng xem xét các ví dụ sau:

Ví dụ 1: Tìm tọa độ tâm đối xứng của đồ thị hàm số y = x³ + 3x² – 9x + 1.

Giải:

1. Tính đạo hàm:

   • y’ = 3x² + 6x – 9
   • y” = 6x + 6

2. Tìm điểm uốn: Giải phương trình y” = 0:

   • 6x + 6 = 0 => x = -1

3. Tìm tọa độ y: Thay x = -1 vào phương trình ban đầu:

   • y = (-1)³ + 3(-1)² – 9(-1) + 1 = 12

4. Kết luận: Vậy tọa độ tâm đối xứng là I(-1, 12).

Ví dụ 2: Tìm tọa độ tâm đối xứng của đồ thị hàm số y = x³ – 3x + 2.

Giải:

1. Tính đạo hàm:

   • y’ = 3x² – 3
   • y” = 6x

2. Tìm điểm uốn: Giải phương trình y” = 0:

   • 6x = 0 => x = 0

3. Tìm tọa độ y: Thay x = 0 vào phương trình ban đầu:

   • y = 0³ – 3(0) + 2 = 2

4. Kết luận: Vậy tọa độ tâm đối xứng là I(0, 2).

5. Ứng Dụng Thực Tế Của Tâm Đối Xứng

Việc xác định tọa độ tâm đối xứng của đồ thị hàm số không chỉ là một bài toán lý thuyết, mà còn có nhiều ứng dụng quan trọng trong thực tế:

• Kiến trúc: Trong thiết kế kiến trúc, việc sử dụng các yếu tố đối xứng tạo ra sự cân bằng và hài hòa cho công trình. Việc xác định tâm đối xứng giúp kiến trúc sư tạo ra những thiết kế đẹp mắt và vững chắc.
• Phân tích dữ liệu: Trong phân tích dữ liệu, việc tìm tâm đối xứng của một tập dữ liệu có thể giúp ta xác định giá trị trung tâm và đánh giá sự phân bố của dữ liệu.
• Tối ưu hóa: Trong các bài toán tối ưu hóa, việc xác định tâm đối xứng có thể giúp ta tìm ra điểm tối ưu một cách nhanh chóng và hiệu quả.
• Vật lý: Trong vật lý, nhiều hiện tượng tự nhiên thể hiện tính đối xứng. Việc nghiên cứu tâm đối xứng giúp chúng ta hiểu rõ hơn về các quy luật vận động của thế giới.

6. Kết Luận

Hiểu rõ về tọa độ tâm đối xứng của đồ thị hàm số là một bước quan trọng để nắm vững kiến thức về hàm số và ứng dụng chúng vào thực tế. Hy vọng rằng, với những kiến thức và ví dụ được trình bày trong bài viết này, bạn đã có thể tự tin xác định tâm đối xứng của đồ thị hàm số và khám phá những ứng dụng thú vị của nó. Chúc bạn thành công trên con đường chinh phục toán học!