Trong hình học không gian, khối trụ là một hình khối quan trọng với nhiều ứng dụng thực tế. Bài viết này sẽ cung cấp kiến thức toàn diện về Tính Thể Tích Khối Trụ, từ định nghĩa, công thức đến các dạng bài tập thường gặp và cách giải quyết chúng.
Khối Trụ Tròn Xoay Là Gì?
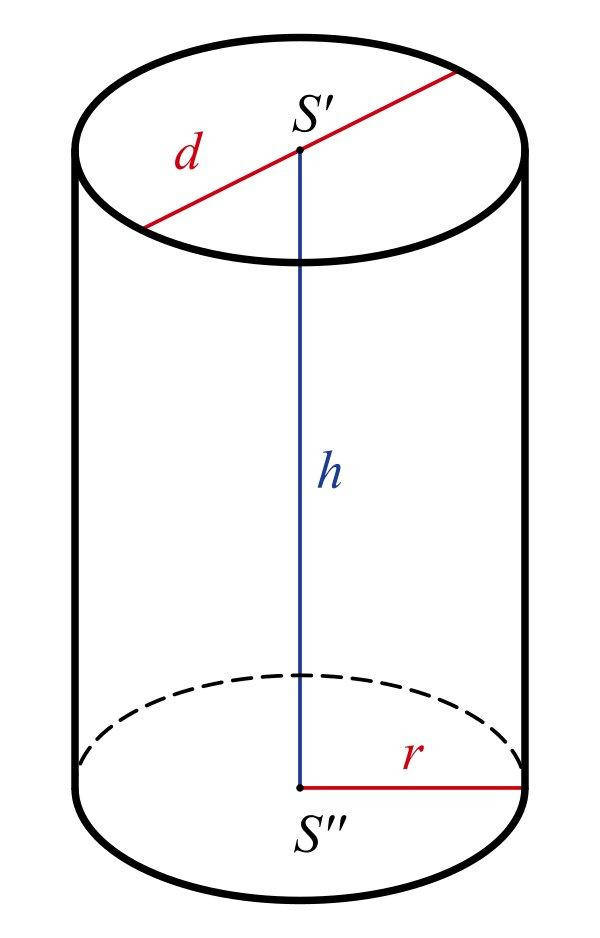
Khối trụ tròn xoay được hình thành khi một hình chữ nhật quay quanh một trong các cạnh của nó. Cạnh quay này trở thành trục của hình trụ, và hai đáy của hình trụ là hai hình tròn bằng nhau nằm trên hai mặt phẳng song song.
Công Thức Tính Thể Tích Khối Trụ
Thể tích khối trụ được tính bằng công thức đơn giản sau:
V = πr²h
Trong đó:
- V: Thể tích khối trụ
- π (pi): Hằng số (xấp xỉ 3.14159)
- r: Bán kính của đáy hình tròn
- h: Chiều cao của khối trụ (khoảng cách giữa hai đáy)
Biểu thức toán học của công thức tính thể tích khối trụ, sử dụng ký hiệu toán học chuẩn để thể hiện rõ ràng mối quan hệ giữa thể tích, bán kính đáy và chiều cao.
Lưu ý: Đơn vị của thể tích phụ thuộc vào đơn vị của bán kính và chiều cao. Ví dụ, nếu bán kính và chiều cao tính bằng mét (m), thì thể tích sẽ tính bằng mét khối (m³).
Các Dạng Bài Tập Về Thể Tích Khối Trụ
Dưới đây là một số dạng bài tập thường gặp về tính thể tích khối trụ và phương pháp giải:
Dạng 1: Tính Bán Kính Đáy (r)
Nếu đề bài cho thể tích (V) và chiều cao (h), ta có thể suy ra bán kính đáy (r) bằng cách biến đổi công thức:
r = √(V / (πh))
Ví dụ: Một khối trụ có thể tích là 100π cm³ và chiều cao là 10 cm. Tính bán kính đáy của khối trụ.
Giải:
r = √(100π / (π * 10)) = √10 cm
Dạng 2: Tính Chiều Cao (h)
Nếu đề bài cho thể tích (V) và bán kính đáy (r), ta có thể suy ra chiều cao (h) bằng cách biến đổi công thức:
h = V / (πr²)
Ví dụ: Một khối trụ có thể tích là 50π m³ và bán kính đáy là 5 m. Tính chiều cao của khối trụ.
Giải:
h = 50π / (π * 5²) = 2 m
Dạng 3: Bài Toán Kết Hợp
Các bài toán phức tạp hơn có thể yêu cầu bạn sử dụng thêm các kiến thức hình học khác (ví dụ: định lý Pythagoras) để tìm ra bán kính đáy hoặc chiều cao trước khi tính thể tích khối trụ.
Bài Tập Vận Dụng
Bài 1: Một hình trụ có trục OO’, bán kính đáy là r và chiều cao h. Một hình vuông ABCD có cạnh bằng a, có hai đỉnh A, B nằm trên đường tròn đáy tâm O, hai đỉnh C, D nằm trên đường tròn đáy tâm O’. Tính thể tích hình trụ theo a.
Hướng dẫn: Xác định mối quan hệ giữa a, r và h thông qua hình vuông ABCD. Sử dụng định lý Pythagoras để tìm mối liên hệ giữa các cạnh của hình vuông và bán kính đáy.
Bài 2: Một cái thùng hình trụ chứa đầy nước, đường kính đáy là 60cm, chiều cao 80cm. Người ta rót hết nước trong thùng ra các can hình trụ có đường kính đáy 10cm, chiều cao 12cm. Hỏi cần ít nhất bao nhiêu can để chứa hết lượng nước đó?
Hướng dẫn: Tính thể tích thùng nước hình trụ lớn và thể tích một can hình trụ nhỏ. Chia thể tích thùng lớn cho thể tích can nhỏ để tìm số can cần thiết.
Ứng Dụng Thực Tế
Tính thể tích khối trụ có nhiều ứng dụng trong thực tế, ví dụ:
- Xây dựng: Tính toán lượng vật liệu cần thiết để xây dựng các cột trụ, bể chứa nước hình trụ,…
- Sản xuất: Tính toán dung tích của các bình chứa, ống dẫn hình trụ,…
- Thiết kế: Thiết kế các sản phẩm có hình dạng trụ như lon nước, hộp đựng,…
Nắm vững công thức và các dạng bài tập về tính thể tích khối trụ sẽ giúp bạn giải quyết các bài toán hình học không gian một cách hiệu quả và ứng dụng kiến thức vào thực tế.