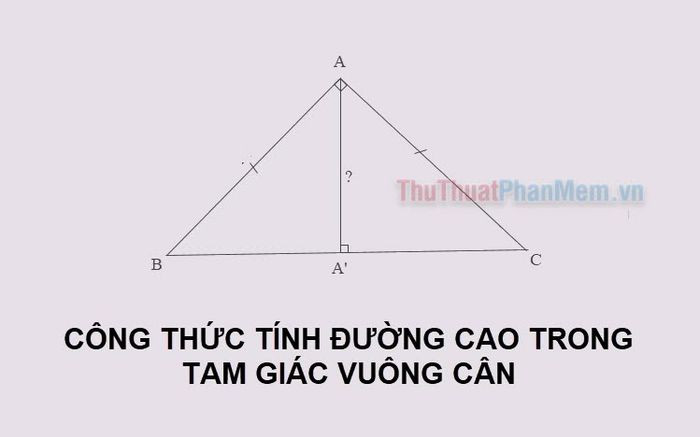
Tam giác vuông cân là một hình học đặc biệt, kết hợp giữa tính chất vuông góc và cân bằng. Việc hiểu rõ về “Tính đường Cao Tam Giác Vuông Cân” là rất quan trọng trong học toán và ứng dụng thực tế.
Đường Cao Trong Tam Giác Vuông Cân Là Gì?
Tam giác vuông cân là tam giác có một góc vuông (90 độ) và hai cạnh góc vuông bằng nhau. Điều này dẫn đến hai góc còn lại bằng 45 độ. Đường cao trong tam giác vuông cân, đặc biệt là đường cao kẻ từ đỉnh góc vuông xuống cạnh huyền, có những tính chất đặc biệt.
Tính Chất Quan Trọng Của Đường Cao Tam Giác Vuông Cân
Đường cao trong tam giác vuông cân không chỉ là đường cao thông thường mà còn mang những đặc điểm riêng:
- Đường trung tuyến: Đường cao đồng thời là đường trung tuyến, chia cạnh huyền thành hai đoạn bằng nhau.
- Đường phân giác: Đường cao cũng là đường phân giác của góc vuông, chia góc vuông thành hai góc 45 độ.
- Đường trung trực: Đường cao cũng là đường trung trực của cạnh huyền, vuông góc và đi qua trung điểm của cạnh huyền.
Công Thức Tính Đường Cao Tam Giác Vuông Cân
Có hai cách chính để tính đường cao trong tam giác vuông cân:
- Khi biết cạnh huyền (BC): Đường cao (AH) bằng một nửa cạnh huyền:
AH = BC / 2 - Khi biết cạnh góc vuông (AB = AC): Áp dụng định lý Pytago để tính cạnh huyền, sau đó sử dụng công thức trên. Hoặc sử dụng công thức trực tiếp:
AH = (AB * căn(2)) / 2
Ví Dụ Minh Họa
Ví dụ 1: Cho tam giác ABC vuông cân tại A, cạnh huyền BC = 8cm. Tính độ dài đường cao AH.
Giải:
Áp dụng công thức: AH = BC / 2 = 8 / 2 = 4cm
Ví dụ 2: Cho tam giác ABC vuông cân tại A, cạnh góc vuông AB = 5cm. Tính độ dài đường cao AH.
Giải:
Cạnh huyền BC = AB * căn(2) = 5 * căn(2)
Áp dụng công thức: AH = BC / 2 = (5 * căn(2)) / 2 ≈ 3.54cm
Ví dụ 3: Cho tam giác vuông cân ABC, độ dài hai cạnh góc vuông AB = AC = 4cm. Tính độ dài đường cao AH.
Giải:
Áp dụng định lý Pytago để tính cạnh huyền BC:
BC = √(AB² + AC²) = √(4² + 4²) = √(32) = 4√2 cm
Độ dài đường cao AH:
AH = 1/2 BC = 1/2 4√2 = 2√2 cm
Ứng Dụng Của Việc Tính Đường Cao Tam Giác Vuông Cân
Việc nắm vững công thức và tính chất của đường cao trong tam giác vuông cân có nhiều ứng dụng:
- Giải toán hình học: Giúp giải các bài toán liên quan đến tính diện tích, chu vi, và các yếu tố khác của tam giác vuông cân.
- Ứng dụng thực tế: Trong xây dựng, kiến trúc, thiết kế, việc tính toán kích thước và các yếu tố liên quan đến tam giác vuông cân là rất quan trọng.
- Lập trình game: Trong lập trình game, việc tính toán khoảng cách và vị trí liên quan đến các đối tượng hình tam giác vuông cân là cần thiết.