Kiến thức về Tính đơn điệu của hàm số là một phần quan trọng trong chương trình Toán lớp 12 và kỳ thi tốt nghiệp THPT. Hiểu rõ về khái niệm này giúp học sinh dễ dàng giải quyết các bài toán liên quan và đạt điểm cao.
1. Lý Thuyết Về Tính Đơn Điệu Của Hàm Số
1.1. Định Nghĩa Tính Đơn Điệu
Cho hàm số y = f(x) xác định trên K (K là một khoảng, đoạn hoặc nửa khoảng):
- Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi x1, x2 thuộc K, x1 < x2 thì f(x1) < f(x2).
- Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi x1, x2 thuộc K, x1 < x2 thì f(x1) > f(x2).
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.
1.2. Điều Kiện Cần và Đủ Để Hàm Số Đơn Điệu
a) Điều kiện cần:
Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
- Nếu hàm số đồng biến trên khoảng K thì f'(x) ≥ 0, với mọi x thuộc K và f'(x) = 0 xảy ra tại một số hữu hạn điểm.
- Nếu hàm số nghịch biến trên khoảng K thì f'(x) ≤ 0, với mọi x thuộc K và f'(x) = 0 xảy ra tại một số hữu hạn điểm.
b) Điều kiện đủ:
Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
- Nếu f'(x) > 0, với mọi x thuộc K thì hàm số đồng biến trên khoảng K.
- Nếu f'(x) < 0, với mọi x thuộc K thì hàm số nghịch biến trên khoảng K.
- Nếu f'(x) = 0, với mọi x thuộc K thì hàm số không đổi trên khoảng K.
2. Quy Tắc Xét Tính Đơn Điệu Của Hàm Số
2.1. Tìm Tập Xác Định
Tìm tập xác định của hàm số y = f(x) là tìm tập giá trị của x để biểu thức f(x) có nghĩa.
- Nếu P(x) là đa thức thì 1/P(x) có nghĩa khi P(x) ≠ 0.
- 1/√P(x) có nghĩa khi P(x) > 0.
- √P(x) có nghĩa khi P(x) ≥ 0.
2.2. Tính Đạo Hàm
Tính đạo hàm f'(x) của hàm số. Bảng công thức đạo hàm cơ bản:
| Hàm số | Đạo hàm |
|---|---|
| x^α | αx^(α-1) |
| √x | 1/(2√x) |
| 1/x | -1/x^2 |
| sinx | cosx |
| cosx | -sinx |
| tanx | 1/cos^2x |
| cotx | -1/sin^2x |
| e^x | e^x |
| a^x | a^x*lna |
| lnx | 1/x |
| log_a(x) | 1/(xlna) |

2.3. Lập Bảng Biến Thiên
- Tìm các nghiệm của phương trình f'(x) = 0.
- Sắp xếp các nghiệm theo thứ tự tăng dần.
- Xét dấu của f'(x) trên các khoảng xác định bởi các nghiệm.
- Dựa vào dấu của f'(x) để kết luận về tính đồng biến, nghịch biến của hàm số.
2.4. Kết Luận Khoảng Đồng Biến, Nghịch Biến
Dựa vào bảng biến thiên để kết luận về khoảng đồng biến, nghịch biến của hàm số.
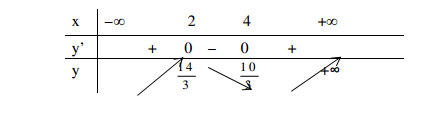
Ví dụ: Xét sự đồng biến, nghịch biến của hàm số y = (1/3)x^3 – 3x^2 + 8x – 2.
- Tập xác định: D = R.
- Đạo hàm: y’ = x^2 – 6x + 8.
- Giải y’ = 0, ta được x = 2 hoặc x = 4.
- Lập bảng biến thiên và kết luận: Hàm số đồng biến trên (-∞; 2) và (4; +∞), nghịch biến trên (2; 4).
3. Các Dạng Bài Tập Về Tính Đơn Điệu Của Hàm Số
3.1. Xét Tính Đơn Điệu Của Hàm Số Chứa Tham Số m
a) Hàm số đồng biến, nghịch biến trên tập xác định:
- Hàm đa thức bậc ba: y = f(x) = ax^3 + bx^2 + cx + d (a ≠ 0).
- Hàm số đồng biến trên R khi và chỉ khi a > 0 và Δ ≤ 0.
- Hàm số nghịch biến trên R khi và chỉ khi a < 0 và Δ ≤ 0.
- Hàm phân thức bậc nhất: y = (ax + b) / (cx + d).
- Hàm số đồng biến trên các khoảng xác định khi y’ > 0 hay (ad – bc) > 0.
- Hàm số nghịch biến trên các khoảng xác định khi y’ < 0 hay (ad – bc) < 0.
Ví dụ: Cho hàm số f(x) = x^3 – 3mx^2 + 3(2m – 1)x + 1. Xác định m để hàm số đồng biến trên tập xác định.
b) Hàm số đồng biến, nghịch biến trên khoảng cho trước:
- Bước 1: Tìm điều kiện của tham số để hàm số xác định trên khoảng (a; b).
- Bước 2: Tính f'(x) và tìm điều kiện của tham số để f'(x) ≥ 0 hoặc f'(x) ≤ 0 trên khoảng (a; b).
Ví dụ: Cho hàm số f(x) = x^3 – 3x^2 – 3(m + 1)x – (m + 1). Tìm m để hàm số đồng biến trên [1; +∞).
3.2. Tính Đơn Điệu Của Hàm Số Chứa Dấu Giá Trị Tuyệt Đối
Tìm khoảng đồng biến, nghịch biến của hàm số y = |f(x)|.
- Bước 1: Khảo sát và lập bảng biến thiên của f(x).
- Bước 2: Dùng phép suy bảng biến thiên của hàm số |f(x)|:
- Giữ nguyên phần nằm trên y = 0.
- Lấy đối xứng qua y = 0 phần bên dưới.
- Bước 3: Nhìn vào bảng biến thiên của |f(x)| suy ra đồng biến, nghịch biến.
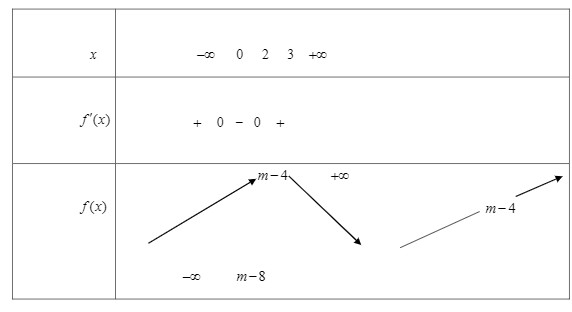
Ví dụ: Tìm tập hợp tất cả các giá trị của tham số m để hàm số y = |x^3 – 3x^2 + m – 4| đồng biến trên (3; +∞).
3.3. Xét Tính Đơn Điệu Của Hàm Số Trên Một Khoảng
Tìm m để hàm số đồng biến/nghịch biến trên [a; b].
- Để hàm số đồng biến trên [a; b] thì f'(x) ≥ 0, ∀x ∈ [a; b].
- Để hàm số nghịch biến trên [a; b] thì f'(x) ≤ 0, ∀x ∈ [a; b].
Ví dụ: Tìm m để hàm số f(x) = x^3 – 3x^2 – 3(m + 1)x – (m + 1) nghịch biến trên [-1; 3].
Bài Tập Về Tính Đơn Điệu Của Hàm Số
(Liệt kê các câu hỏi trắc nghiệm như trong bài gốc)
Nắm vững lý thuyết và luyện tập các dạng bài tập khác nhau sẽ giúp bạn tự tin giải quyết các bài toán về tính đơn điệu của hàm số trong kỳ thi. Chúc bạn thành công!
