Việc Tính Diện Tích Miền Nghiệm Của Hệ Bất Phương Trình là một bài toán thường gặp trong chương trình Toán học phổ thông và có nhiều ứng dụng thực tế. Bài viết này sẽ trình bày chi tiết phương pháp giải và các ví dụ minh họa để bạn đọc dễ dàng nắm bắt.
Xét một hệ bất phương trình bậc nhất hai ẩn, miền nghiệm của hệ là giao của các miền nghiệm của từng bất phương trình trong hệ. Miền nghiệm này thường là một đa giác (lồi hoặc không lồi).
Để tính diện tích miền nghiệm của hệ bất phương trình, ta thực hiện các bước sau:
- Xác định miền nghiệm: Vẽ đồ thị biểu diễn miền nghiệm của từng bất phương trình trong hệ. Miền nghiệm của hệ là phần giao của tất cả các miền nghiệm này. Thông thường, ta sẽ gạch bỏ các phần không thuộc miền nghiệm để phần còn lại là miền nghiệm cần tìm.
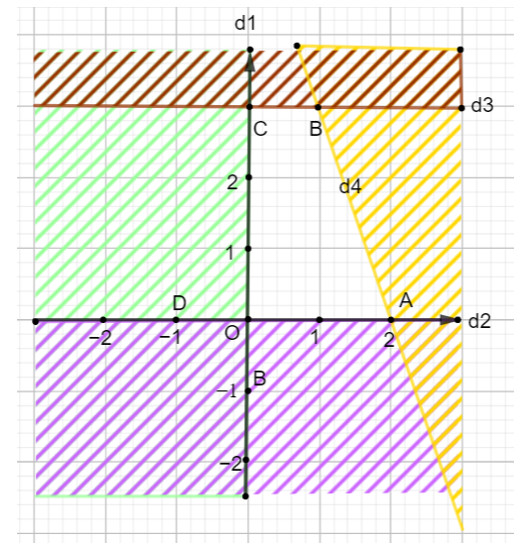Hình ảnh miền nghiệm là phần không bị gạch, minh họa tính diện tích hình thang vuông
-
Xác định các đỉnh của đa giác: Tìm tọa độ các giao điểm của các đường thẳng là biên của miền nghiệm. Các giao điểm này chính là các đỉnh của đa giác tạo thành miền nghiệm.
-
Tính diện tích đa giác: Có nhiều cách để tính diện tích đa giác, tùy thuộc vào hình dạng của nó. Một số phương pháp phổ biến bao gồm:
-
Chia đa giác thành các hình đơn giản: Chia đa giác thành các tam giác, hình chữ nhật, hình thang,… có diện tích dễ tính, sau đó tính tổng diện tích của các hình này.
-
Sử dụng công thức Gauss (công thức diện tích Shoelace): Cho đa giác có các đỉnh lần lượt là (x1, y1), (x2, y2), …, (xn, yn), diện tích của đa giác được tính theo công thức:
S = 1/2 * |(x1y2 + x2y3 + … + xn-1yn + xny1) – (y1x2 + y2x3 + … + yn-1xn + ynx1)|
-
Sử dụng tích phân (nếu đường biên được biểu diễn bằng hàm số): Trong một số trường hợp, miền nghiệm có thể được giới hạn bởi các đường cong biểu diễn bằng hàm số. Khi đó, ta có thể sử dụng tích phân để tính diện tích.
-
Ví dụ:
Cho hệ bất phương trình:
- x ≥ 0
- y ≥ 0
- x + y ≤ 3
- x + 2y ≤ 4
Hãy tính diện tích miền nghiệm của hệ bất phương trình này.
Giải:
-
Xác định miền nghiệm: Vẽ các đường thẳng x = 0, y = 0, x + y = 3 và x + 2y = 4. Miền nghiệm là miền đa giác giới hạn bởi các đường thẳng này và nằm trong góc phần tư thứ nhất.
-
Xác định các đỉnh của đa giác: Các đỉnh của đa giác là:
- A(0, 0)
- B(3, 0)
- C(2, 1) (giao điểm của x + y = 3 và x + 2y = 4)
- D(0, 2)
-
Tính diện tích đa giác: Ta có thể chia đa giác ABCD thành tam giác OAB và tam giác BCD. Hoặc sử dụng công thức Gauss cho tứ giác ABCD.
Áp dụng công thức Gauss:
S = 1/2 |(00 + 31 + 22 + 00) – (03 + 02 + 10 + 2*0)|
S = 1/2 * |(0 + 3 + 4 + 0) – (0 + 0 + 0 + 0)|
S = 1/2 * |7| = 3.5
Vậy, diện tích miền nghiệm của hệ bất phương trình là 3.5 đơn vị diện tích.
Khi gặp bài toán tính diện tích miền nghiệm của hệ bất phương trình, việc quan trọng nhất là xác định đúng miền nghiệm và lựa chọn phương pháp tính diện tích phù hợp. Việc luyện tập thường xuyên với nhiều dạng bài khác nhau sẽ giúp bạn nâng cao kỹ năng giải toán và đạt kết quả tốt.
