Hình quạt tròn là một phần quan trọng của hình học, xuất hiện nhiều trong các bài toán và ứng dụng thực tế. Bài viết này sẽ cung cấp đầy đủ kiến thức về Tính Diện Tích Hình Quạt Tròn, các dạng bài tập thường gặp và ví dụ minh họa chi tiết, giúp bạn nắm vững và áp dụng thành thạo.
Công Thức Tính Diện Tích Hình Quạt Tròn
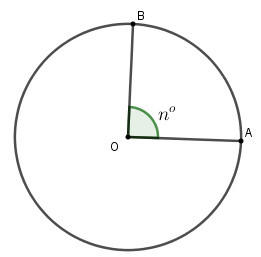
Diện tích hình quạt tròn phụ thuộc vào bán kính và góc ở tâm của nó. Dưới đây là các công thức chính:
-
Công thức 1: Sử dụng bán kính và góc ở tâm (độ)
(S = dfrac{{pi R^2 n}}{{360}})
Trong đó:
Slà diện tích hình quạt tròn.Rlà bán kính của đường tròn.nlà số đo góc ở tâm (tính bằng độ).
-
Công thức 2: Sử dụng bán kính và độ dài cung
(S = dfrac{{l cdot R}}{2})
Trong đó:
Slà diện tích hình quạt tròn.Rlà bán kính của đường tròn.llà độ dài cung của hình quạt tròn.
Lưu ý: Cần đảm bảo đơn vị đo của bán kính và độ dài cung là thống nhất trước khi áp dụng công thức.
Các Dạng Toán Thường Gặp về Tính Diện Tích Hình Quạt Tròn
-
Tính diện tích hình tròn, diện tích hình quạt tròn và các đại lượng liên quan: Dạng bài tập này thường yêu cầu áp dụng trực tiếp các công thức đã nêu trên.
-
Bài toán tổng hợp: Dạng bài này đòi hỏi sự linh hoạt trong việc sử dụng các kiến thức về góc ở tâm, bán kính đường tròn, và các tính chất hình học khác để giải quyết.
Bài Tập Vận Dụng
Câu 1. Cho đường tròn (O) bán kính 10 cm. Tính diện tích hình quạt tròn AOM, biết góc AOM = 90 độ.
Lời giải:
Áp dụng công thức: (S = dfrac{{pi R^2 n}}{{360}})
Ta có: R = 10 cm, n = 90 độ
Suy ra: (S = dfrac{{pi cdot 10^2 cdot 90}}{{360}} = 25pi ,(cm^2))
Vậy diện tích hình quạt tròn AOM là (25pi ,cm^2).
Câu 2. Cho đường tròn (O) đường kính AB = 4√3 cm. Điểm C thuộc (O) sao cho góc ABC = 30 độ. Tính diện tích hình viên phân AC. (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy).
Lời giải:
- Tính góc ở tâm AOC: (widehat {AOC} = 2.widehat {ABC} = {2.30^0} = {60^0})
- Tính diện tích hình quạt tròn AOC: ({S_{qAOC}} = dfrac{{pi {R^2}.60}}{{360}} = dfrac{{pi {R^2}}}{6})
- Tính diện tích tam giác AOC (tam giác đều): ({S_{AOC}} = dfrac{{sqrt 3 }}{4}.{R^2}.)
- Tính diện tích hình viên phân AC: ({S_{qAOC}} – {S_{AOC}} = dfrac{{pi {R^2}}}{6} – dfrac{{sqrt 3 }}{4}.{R^2} = left( {dfrac{pi }{6} – dfrac{{sqrt 3 }}{4}} right).{R^2} )
Thay R = 2√3, ta được kết quả: (2pi – 3sqrt 3 , cm^2.)
Câu 3. Tại một vòng xoay ngã tư, người ta cần làm các bồn trồng hoa như hình. Em hãy tính phần diện tích của 1 bồn hoa ở hình (phần được tô đậm). Biết rằng bán kính của vòng tròn lớn là 7m, vòng tròn nhỏ là 3m, số đo cung tròn đó là 60°.
Lời giải:
- Diện tích hình quạt tròn lớn: (frac{{pi {{.7}^2}.60}}{{360}} = frac{{49pi }}{6}left( {{m^2}} right))
- Diện tích hình quạt tròn nhỏ: (frac{{pi {{.3}^2}.60}}{{360}} = frac{{3pi }}{2}left( {{m^2}} right))
- Diện tích phần bồn hoa: (frac{{49pi }}{6} – frac{{3pi }}{2} = frac{{20pi }}{3} approx 20,9left( {{m^2}} right))
Câu 4. Cho đường tròn (O) đường kính AB = 2√2 cm. Điểm C thuộc (O) sao cho góc ABC = 30°. Tính diện tích hình giới hạn bởi đường tròn (O) và AC, BC.
Lời giải:
- Tính diện tích hình tròn (O): ({S_{(O)}} = pi {R^2})
- Chứng minh tam giác AOC đều và tính diện tích tam giác ABC.
- Tính diện tích hình giới hạn: (dfrac{1}{2}{S_{(O)}} – {S_{ABC}} = dfrac{1}{2}left( {pi – sqrt 3 } right){R^2} = pi – sqrt 3 .)
Ứng Dụng Thực Tế của Việc Tính Diện Tích Hình Quạt Tròn
- Kiến trúc và xây dựng: Tính toán diện tích các chi tiết trang trí hình quạt, thiết kế mái vòm,…
- Thiết kế và trang trí: Tạo ra các họa tiết, hoa văn hình quạt trong thiết kế đồ họa, nội thất,…
- Nông nghiệp: Tính toán diện tích tưới tiêu của các hệ thống phun nước theo hình quạt.
Kết luận
Việc nắm vững công thức và các dạng bài tập về tính diện tích hình quạt tròn sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và ứng dụng vào thực tế một cách hiệu quả. Hy vọng bài viết này cung cấp cho bạn những kiến thức hữu ích và cần thiết.