Hình ngũ giác là một hình đa giác có 5 cạnh và 5 góc. Việc Tính Diện Tích Hình Ngũ Giác có thể gây khó khăn, đặc biệt với các hình ngũ giác không đều. Bài viết này sẽ cung cấp đầy đủ thông tin về cách tính diện tích hình ngũ giác, từ cơ bản đến nâng cao, giúp bạn giải quyết các bài tập một cách hiệu quả.
Hình Ngũ Giác Là Gì?
Hình ngũ giác là một hình đa giác hai chiều được tạo thành từ năm cạnh thẳng nối với nhau, tạo thành năm góc.
Có hai loại hình ngũ giác chính:
- Ngũ giác đều: Là hình ngũ giác có tất cả các cạnh và góc bằng nhau. Mỗi góc trong của ngũ giác đều là 108 độ.
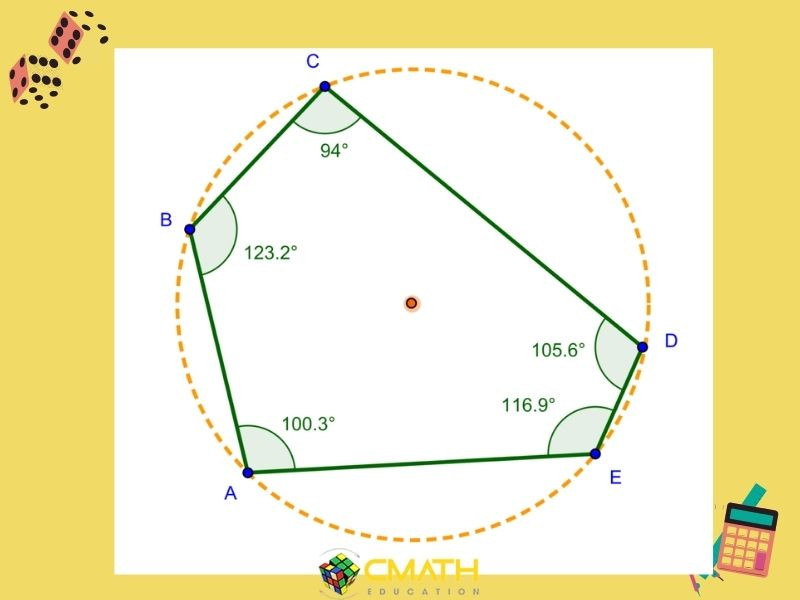
- Ngũ giác không đều: Là hình ngũ giác có các cạnh và góc không bằng nhau.
Tổng số đo các góc trong của một ngũ giác bất kỳ luôn là 540 độ.
Công Thức Tính Diện Tích Hình Ngũ Giác
Việc tính diện tích hình ngũ giác phụ thuộc vào việc đó là ngũ giác đều hay không đều.
Diện Tích Ngũ Giác Đều
Ngũ giác đều có tất cả các cạnh và góc bằng nhau. Công thức tính diện tích ngũ giác đều như sau:
S = (5 * a^2) / (4 * tan(π/5))Trong đó:
- S: Diện tích của ngũ giác đều.
- a: Độ dài một cạnh của ngũ giác đều.
- π: Hằng số Pi (xấp xỉ 3.14159).
Ví dụ: Tính diện tích ngũ giác đều có cạnh dài 7cm.
S = (5 7^2) / (4 tan(π/5)) ≈ 84.3 cm²
Diện Tích Ngũ Giác Không Đều
Ngũ giác không đều là hình có 5 cạnh và 5 góc không bằng nhau. Không có công thức chung để tính diện tích ngũ giác không đều. Cách tiếp cận phổ biến nhất là chia ngũ giác thành các hình tam giác nhỏ hơn.
Các bước thực hiện:
- Chia ngũ giác: Chia ngũ giác không đều thành ba tam giác bằng cách nối các đỉnh không kề nhau.
- Tính diện tích từng tam giác: Sử dụng công thức tính diện tích tam giác (S = 1/2 đáy chiều cao) để tính diện tích của mỗi tam giác.
- Cộng diện tích các tam giác: Cộng diện tích của ba tam giác lại với nhau để được diện tích của ngũ giác không đều.
Công thức tính diện tích tam giác khi biết tọa độ ba đỉnh (x1, y1), (x2, y2), (x3, y3) là:
S = 1/2 * |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|
Ứng Dụng của Hình Ngũ Giác Trong Thực Tế
Hình ngũ giác xuất hiện trong nhiều lĩnh vực khác nhau:
- Kiến trúc: Thiết kế mặt bằng, cửa sổ, hoặc các yếu tố trang trí.
- Thiết kế: Logo, biểu tượng, và các mẫu trang trí.
- Tự nhiên: Một số loài hoa, cấu trúc tinh thể.
- Toán học và giáo dục: Các bài toán hình học, nghiên cứu về đa giác.
Nâng Cao Kỹ Năng Giải Toán Diện Tích Ngũ Giác
Để chinh phục các bài toán phức tạp về diện tích ngũ giác, việc nắm vững kiến thức cơ bản về hình học, đặc biệt là hình tam giác, là rất quan trọng. Ngoài ra, việc luyện tập thường xuyên với nhiều dạng bài tập khác nhau cũng giúp bạn rèn luyện tư duy và kỹ năng giải toán.