Trong hình học tam giác, ngoài tính chất đường phân giác trong, Tính Chất Tia Phân Giác Ngoài đóng vai trò quan trọng trong việc giải các bài toán liên quan đến tỉ lệ đoạn thẳng và chứng minh hình học. Bài viết này sẽ đi sâu vào lý thuyết và các dạng bài tập thường gặp liên quan đến tính chất này.
1. Định Lý Về Tia Phân Giác Ngoài
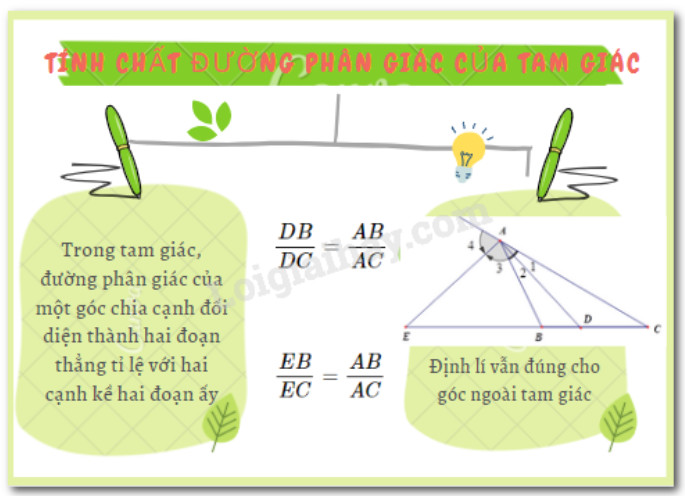
Định lý phát biểu rằng: Tia phân giác của góc ngoài tại một đỉnh của tam giác chia cạnh đối diện thành hai đoạn thẳng, mà tỉ lệ độ dài của chúng bằng tỉ lệ độ dài hai cạnh kề với đỉnh đó.
Alt: Biểu tượng chú ý, nhấn mạnh về định lý đường phân giác trong tam giác
2. Biểu Diễn Toán Học
Xét tam giác (ABC) với (AE) là tia phân giác của góc ngoài tại đỉnh (A) (E nằm trên đường thẳng BC). Khi đó, ta có tỉ lệ thức sau:
$dfrac{{EB}}{{EC}} = dfrac{{AB}}{{AC}}$
3. Ví Dụ Minh Họa
Cho tam giác (ABC) có (AD) là đường phân giác trong và (AE) là đường phân giác ngoài tại đỉnh (A). Khi đó, ta có:
- $dfrac{{DB}}{{DC}} = dfrac{{AB}}{{AC}}$ (tính chất đường phân giác trong)
- $dfrac{{EB}}{{EC}} = dfrac{{AB}}{{AC}}$ (tính chất đường phân giác ngoài)
4. Các Dạng Toán Thường Gặp và Phương Pháp Giải
Dạng 1: Tính Độ Dài Cạnh
Sử dụng tính chất tia phân giác ngoài và các tỉ lệ thức để thiết lập mối quan hệ giữa các cạnh và đoạn thẳng, từ đó tính toán độ dài các cạnh chưa biết.
Ví dụ: Cho tam giác ABC, AB = 6cm, AC = 8cm, BC = 10cm. Tia phân giác ngoài tại A cắt đường thẳng BC tại E. Tính độ dài BE và CE.
Giải:
Áp dụng tính chất tia phân giác ngoài, ta có: (dfrac{EB}{EC} = dfrac{AB}{AC} = dfrac{6}{8} = dfrac{3}{4})
Đặt EB = 3x, EC = 4x. Vì E nằm ngoài đoạn BC nên EC – EB = BC, hay 4x – 3x = 10, suy ra x = 10.
Vậy BE = 3x = 30cm, CE = 4x = 40cm.
Dạng 2: Chứng Minh Đẳng Thức Hình Học
Sử dụng tính chất tia phân giác ngoài để chứng minh các đẳng thức liên quan đến tỉ lệ đoạn thẳng, sự đồng quy của các đường thẳng, hoặc các tính chất hình học khác.
Hình minh họa bài toán chứng minh liên quan đến đường phân giác ngoài
Alt: Hình vẽ minh họa bài toán chứng minh tính chất đường phân giác trong và ngoài của tam giác.
Ví dụ: Cho tam giác ABC. Chứng minh rằng giao điểm của đường phân giác trong tại A và đường phân giác ngoài tại A nằm trên đường tròn đường kính BC (với điều kiện là AB khác AC).
5. Ứng Dụng Thực Tế
Tính chất tia phân giác ngoài không chỉ là một khái niệm lý thuyết mà còn được ứng dụng trong nhiều bài toán thực tế liên quan đến đo đạc, thiết kế và xây dựng. Ví dụ, trong việc thiết kế các công trình kiến trúc có tính đối xứng hoặc trong các bài toán về định vị.
Kết luận:
Hiểu rõ tính chất tia phân giác ngoài của tam giác là một lợi thế lớn trong việc giải quyết các bài toán hình học. Việc nắm vững lý thuyết và luyện tập các dạng bài tập khác nhau sẽ giúp bạn tự tin hơn khi đối diện với các thử thách hình học phức tạp.