Tam giác cân là một hình học cơ bản nhưng lại chứa đựng nhiều tính chất thú vị và quan trọng, đặc biệt là liên quan đến đường cao. Bài viết này sẽ đi sâu vào những tính chất đó, đồng thời cung cấp các công thức và ví dụ minh họa để giúp bạn nắm vững kiến thức.
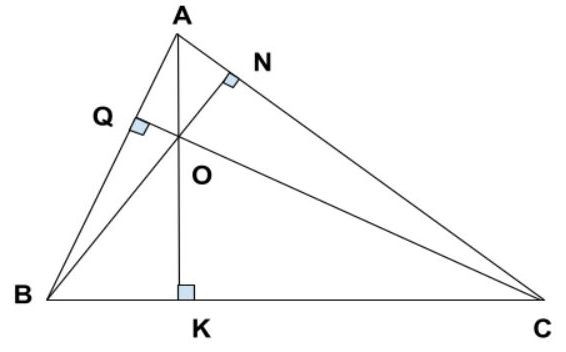
Hình ảnh minh họa đường cao trong tam giác thường, giúp học sinh hình dung rõ hơn về khái niệm.
1. Định Nghĩa và Tính Chất Cơ Bản của Tam Giác Cân
Tam giác cân là tam giác có hai cạnh bên bằng nhau. Hai góc ở đáy của tam giác cân cũng bằng nhau. Đây là những kiến thức nền tảng quan trọng để hiểu sâu hơn về các tính chất liên quan đến đường cao.
1.1. Đường Cao trong Tam Giác Cân: Vai Trò và Đặc Điểm
Đường cao trong tam giác cân là đoạn thẳng kẻ từ đỉnh của tam giác vuông góc xuống cạnh đối diện. Tuy nhiên, không phải đường cao nào cũng có vai trò như nhau.
- Đường cao xuất phát từ đỉnh cân: Đây là đường cao đặc biệt quan trọng, đồng thời là đường trung tuyến, đường trung trực và đường phân giác của góc ở đỉnh. Điều này có nghĩa là nó chia cạnh đáy thành hai đoạn bằng nhau và chia góc ở đỉnh thành hai góc bằng nhau.
- Hai đường cao xuất phát từ hai đỉnh đáy: Hai đường cao này bằng nhau.
1.2. Tính Chất Đặc Biệt Của Đường Cao Xuất Phát Từ Đỉnh Cân
Đường cao xuất phát từ đỉnh cân có những tính chất vô cùng quan trọng:
- Tính chất trung tuyến: Đường cao này đồng thời là đường trung tuyến, chia cạnh đáy thành hai phần bằng nhau.
- Tính chất phân giác: Đường cao này đồng thời là đường phân giác, chia góc ở đỉnh thành hai góc bằng nhau.
- Tính chất đường trung trực: Đường cao này đồng thời là đường trung trực của cạnh đáy, tức là nó vuông góc với cạnh đáy tại trung điểm của cạnh đáy.
Hình ảnh trực quan về đường cao trong tam giác cân, thể hiện rõ tính chất vừa là đường cao, đường trung tuyến, đường trung trực và đường phân giác.
2. Công Thức Tính Đường Cao trong Tam Giác Cân
Để giải các bài toán liên quan đến tam giác cân, việc nắm vững công thức tính đường cao là rất quan trọng.
2.1. Công Thức Tổng Quát
Giả sử tam giác cân ABC có AB = AC = a, BC = b. Gọi h là độ dài đường cao AH kẻ từ đỉnh A xuống cạnh BC. Khi đó, ta có công thức:
h = √(a² – (b/2)²)
Công thức này được suy ra từ định lý Pythagoras trong tam giác vuông AHB (hoặc AHC).
2.2. Ví Dụ Minh Họa
Cho tam giác cân ABC có AB = AC = 5cm, BC = 6cm. Tính độ dài đường cao AH.
Áp dụng công thức trên, ta có:
h = √(5² – (6/2)²) = √(25 – 9) = √16 = 4cm
Vậy độ dài đường cao AH là 4cm.
3. Ứng Dụng của Tính Chất Đường Cao trong Giải Toán
Các tính chất của đường cao trong tam giác cân được ứng dụng rộng rãi trong giải toán hình học, đặc biệt là các bài toán chứng minh và tính toán.
3.1. Chứng Minh Các Tính Chất Hình Học
Ví dụ: Cho tam giác ABC cân tại A. Gọi H là trung điểm của BC. Chứng minh rằng AH là đường cao của tam giác ABC.
Chứng minh:
- Vì H là trung điểm của BC nên BH = HC.
- Xét hai tam giác AHB và AHC, ta có:
- AB = AC (tam giác ABC cân tại A)
- BH = HC (H là trung điểm của BC)
- AH là cạnh chung
- Do đó, tam giác AHB bằng tam giác AHC (c.c.c).
- Suy ra góc AHB bằng góc AHC.
- Mà góc AHB + góc AHC = 180° (hai góc kề bù).
- Vậy góc AHB = góc AHC = 90°.
- Do đó, AH vuông góc với BC.
- Vậy AH là đường cao của tam giác ABC.
3.2. Giải Các Bài Toán Tính Toán
Ví dụ: Cho tam giác ABC cân tại A, có góc A bằng 30 độ, cạnh BC = 8cm. Tính độ dài đường cao AH.
Giải:
- Vì tam giác ABC cân tại A nên góc B = góc C = (180° – 30°)/2 = 75°.
- Xét tam giác vuông AHB, ta có:
- sinB = AH/AB
- => AH = AB * sinB
- Để tính AB, ta sử dụng định lý sin trong tam giác ABC:
- BC/sinA = AB/sinC
- => AB = (BC sinC)/sinA = (8 sin75°)/sin30° ≈ 15.45cm
- Vậy AH ≈ 15.45 * sin75° ≈ 14.93cm.
4. Mở Rộng: Tam Giác Vuông Cân
Tam giác vuông cân là một trường hợp đặc biệt của tam giác cân, vừa có tính chất của tam giác cân, vừa có tính chất của tam giác vuông. Trong tam giác vuông cân, đường cao ứng với cạnh huyền đồng thời là đường trung tuyến và bằng một nửa cạnh huyền.
Hình ảnh minh họa cách tính đường cao trong tam giác đều, một trường hợp đặc biệt liên quan đến tam giác cân.
5. Kết Luận
Hiểu rõ tính chất tam giác cân và đường cao là vô cùng quan trọng trong học toán hình học. Việc nắm vững các kiến thức này không chỉ giúp bạn giải quyết các bài toán một cách dễ dàng mà còn giúp bạn phát triển tư duy logic và khả năng suy luận. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng chúng một cách linh hoạt trong các bài toán khác nhau.