Hình lăng trụ đều là một dạng hình học không gian đặc biệt, đóng vai trò quan trọng trong chương trình toán học phổ thông và ứng dụng thực tế. Bài viết này sẽ đi sâu vào định nghĩa, tính chất và các công thức liên quan đến hình lăng trụ đều, giúp bạn nắm vững kiến thức và giải quyết các bài toán liên quan một cách hiệu quả.
Hình Lăng Trụ Đều Là Gì?
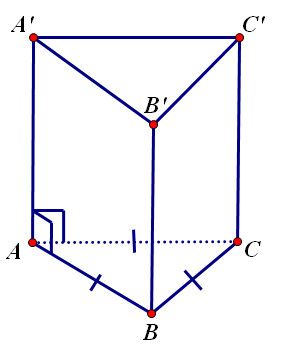
Hình lăng trụ đều là hình lăng trụ đứng có đáy là một đa giác đều. Điều này có nghĩa là tất cả các cạnh đáy và các góc ở đáy đều bằng nhau. Hình lăng trụ đều có các mặt bên là các hình chữ nhật bằng nhau và vuông góc với mặt đáy.
Các Loại Hình Lăng Trụ Đều Phổ Biến
Tùy thuộc vào hình dạng của đa giác đáy, chúng ta có các loại hình lăng trụ đều khác nhau, phổ biến nhất là:
- Hình lăng trụ tam giác đều: Đáy là tam giác đều.
- Hình lăng trụ tứ giác đều (hình hộp chữ nhật): Đáy là hình vuông.
- Hình lăng trụ ngũ giác đều: Đáy là ngũ giác đều.
- Hình lăng trụ lục giác đều: Đáy là lục giác đều.
Tính Chất Đặc Trưng Của Hình Lăng Trụ Đều
Hình lăng trụ đều sở hữu những tính chất hình học quan trọng, giúp chúng ta nhận biết và tính toán các yếu tố liên quan:
- Đáy là đa giác đều: Các cạnh và góc của đa giác đáy bằng nhau.
- Các mặt bên là hình chữ nhật: Các mặt bên đều là hình chữ nhật và có diện tích bằng nhau.
- Các cạnh bên bằng nhau và vuông góc với đáy: Các cạnh bên có độ dài bằng nhau và tạo thành góc vuông với mặt phẳng đáy.
- Tính đối xứng cao: Hình lăng trụ đều có trục đối xứng đi qua tâm của hai đáy.
Công Thức Tính Thể Tích và Diện Tích Hình Lăng Trụ Đều
Để giải các bài toán liên quan đến hình lăng trụ đều, chúng ta cần nắm vững các công thức tính thể tích và diện tích:
Thể Tích (V)
Thể tích của hình lăng trụ đều được tính bằng công thức:
V = S_đáy * hTrong đó:
S_đáy: Diện tích đáy của hình lăng trụ đều.h: Chiều cao của hình lăng trụ đều (khoảng cách giữa hai đáy).
Ví dụ, đối với hình lăng trụ tam giác đều có cạnh đáy là a và chiều cao là h, diện tích đáy là (a^2 * √3) / 4, do đó thể tích là V = ((a^2 * √3) / 4) * h.
Diện Tích Xung Quanh (Sxq)
Diện tích xung quanh của hình lăng trụ đều là tổng diện tích của các mặt bên:
Sxq = P_đáy * hTrong đó:
P_đáy: Chu vi đáy của hình lăng trụ đều.h: Chiều cao của hình lăng trụ đều.
Ví dụ, đối với hình lăng trụ tam giác đều có cạnh đáy là a và chiều cao là h, chu vi đáy là 3a, do đó diện tích xung quanh là Sxq = 3a * h.
Diện Tích Toàn Phần (Stp)
Diện tích toàn phần của hình lăng trụ đều là tổng diện tích xung quanh và diện tích của hai đáy:
Stp = Sxq + 2 * S_đáyBài Tập Vận Dụng Về Hình Lăng Trụ Đều
Để củng cố kiến thức, chúng ta hãy cùng xét một số bài tập ví dụ:
Bài 1: Một hình lăng trụ tam giác đều có cạnh đáy là 5cm và chiều cao là 8cm. Tính thể tích của hình lăng trụ này.
Giải:
- Diện tích đáy:
S_đáy = (5^2 * √3) / 4 = (25√3) / 4 cm^2 - Thể tích:
V = S_đáy * h = ((25√3) / 4) * 8 = 50√3 cm^3
Bài 2: Một hình lăng trụ tứ giác đều có cạnh đáy là 4cm và diện tích xung quanh là 96cm². Tính chiều cao của hình lăng trụ.
Giải:
- Chu vi đáy:
P_đáy = 4 * 4 = 16 cm - Diện tích xung quanh:
Sxq = P_đáy * h => 96 = 16 * h => h = 6 cm
Ứng Dụng Thực Tế Của Hình Lăng Trụ Đều
Hình lăng trụ đều không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng thực tế trong đời sống và kỹ thuật:
- Kiến trúc: Các tòa nhà, cột trụ, mái nhà có thể được thiết kế dựa trên hình dạng lăng trụ đều để đảm bảo tính vững chắc và thẩm mỹ.
- Xây dựng: Các khối bê tông, vật liệu xây dựng có thể được đúc theo hình lăng trụ đều để dễ dàng lắp ghép và chịu lực tốt.
- Thiết kế sản phẩm: Nhiều sản phẩm gia dụng, đồ trang trí, hộp đựng được thiết kế theo hình lăng trụ đều để tối ưu hóa không gian và tạo hình dáng hấp dẫn.
Kết Luận
Hiểu rõ về Tính Chất Hình Lăng Trụ đều là rất quan trọng để giải quyết các bài toán hình học không gian và ứng dụng vào thực tế. Hy vọng bài viết này đã cung cấp cho bạn đầy đủ kiến thức cần thiết về hình lăng trụ đều, từ định nghĩa, tính chất đến các công thức tính toán và ứng dụng thực tế. Chúc bạn học tốt và thành công!