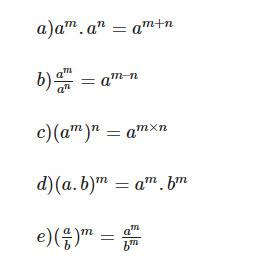Hàm số mũ là một chủ đề quan trọng trong chương trình Toán 12. Để nắm vững kiến thức và giải quyết các bài tập liên quan một cách hiệu quả, việc hiểu rõ các tính chất của hàm số mũ là vô cùng cần thiết. Bài viết này sẽ cung cấp một cái nhìn toàn diện và sâu sắc về chủ đề này.
Hình ảnh minh họa tổng quan về hàm số mũ và lũy thừa, mối liên hệ giữa chúng và các yếu tố cần nắm vững.
1. Nền Tảng Vững Chắc: Lũy Thừa
Để hiểu sâu sắc về hàm số mũ, chúng ta cần bắt đầu từ khái niệm lũy thừa. Hàm số mũ thực chất là một dạng phát triển của lũy thừa, do đó, việc nắm vững các tính chất và công thức biến đổi của lũy thừa sẽ giúp ích rất nhiều trong việc tiếp cận và giải quyết các bài toán liên quan đến hàm số mũ.
1.1. Định Nghĩa Lũy Thừa
Lũy thừa là một phép toán biểu diễn sự nhân lặp đi lặp lại của một số. Với cơ số $a$ và số mũ $n$, lũy thừa được ký hiệu là $a^n$, trong đó $n$ là số lần $a$ được nhân với chính nó.
1.2. Các Tính Chất Quan Trọng Của Lũy Thừa
Các tính chất của lũy thừa đóng vai trò then chốt trong việc biến đổi và tính toán các biểu thức chứa hàm số mũ.
- Tính chất về đẳng thức: Cho $a neq 0; b neq 0; m, n in mathbb{R}$, ta có:
Hình ảnh minh họa các tính chất cơ bản của lũy thừa như nhân chia lũy thừa cùng cơ số, lũy thừa của một tích, lũy thừa của lũy thừa.
-
Tính chất về bất đẳng thức:
-
So sánh cùng cơ số: Cho $m, n in mathbb{R}$. Khi đó:
-
Với $a > 1$ thì $a^m > a^n Rightarrow m > n$
-
Với $0 < a < 1$ thì $a^m > a^n Rightarrow m < n$
-
-
So sánh cùng số mũ:
-
Với số mũ dương $n > 0$: $a > b > 0 Rightarrow a^n > b^n$
-
Với số mũ âm $n < 0$: $a > b > 0 Rightarrow a^n < b^n$
-
-
2. Khám Phá Hàm Số Mũ
2.1. Định Nghĩa Hàm Số Mũ
Hàm số mũ là hàm số có dạng $y = f(x) = a^x$, trong đó $a$ là một số thực dương khác 1 và $x$ là biến số thực. Điều kiện $a > 0$ và $a neq 1$ là vô cùng quan trọng để đảm bảo hàm số mũ có những tính chất đặc trưng.
2.2. Các Tính Chất Quan Trọng Của Hàm Số Mũ
Hiểu rõ các tính chất của hàm số mũ là chìa khóa để giải quyết các bài toán liên quan.
Hình ảnh liệt kê các tính chất của hàm số mũ, bao gồm tập xác định, tập giá trị, tính đơn điệu (đồng biến, nghịch biến) và các điểm đặc biệt trên đồ thị.
Xét hàm số $y = a^x$ với $a > 0$, $a neq 1$:
- Tập xác định: $D = mathbb{R}$
- Tập giá trị: $T = (0; +infty)$
- Tính đơn điệu:
- Nếu $a > 1$ thì hàm số đồng biến trên $mathbb{R}$.
- Nếu $0 < a < 1$ thì hàm số nghịch biến trên $mathbb{R}$.
- Đồ thị:
- Đồ thị hàm số có tiệm cận ngang $y = 0$ (trục hoành).
- Đồ thị hàm số luôn đi qua các điểm $(0; 1)$ và $(1; a)$.
- Đồ thị nằm hoàn toàn phía trên trục hoành vì $a^x > 0, forall x in mathbb{R}$.
2.3. Khảo Sát Và Vẽ Đồ Thị Hàm Số Mũ
Việc khảo sát và vẽ đồ thị hàm số mũ giúp chúng ta hình dung rõ hơn về sự biến thiên và các đặc điểm của hàm số.
- Tập xác định: $D = mathbb{R}$
- Chiều biến thiên:
- Nếu $a > 1$ thì hàm số đồng biến trên $mathbb{R}$.
- Nếu $0 < a < 1$ thì hàm số nghịch biến trên $mathbb{R}$.
- Đồ thị:
- Đồ thị hàm số có tiệm cận ngang $y = 0$
- Đồ thị hàm số luôn đi qua các điểm $(0; 1)$ và $(1; a)$
- Đồ thị nằm hoàn toàn trên phía trục hoành vì $a^x > 0$, $x in mathbb{R}$
Hình ảnh thể hiện rõ sự khác biệt giữa đồ thị hàm số mũ khi a > 1 và 0 < a < 1, nhấn mạnh tính đồng biến và nghịch biến.
3. Ứng Dụng Thực Tế: Các Dạng Bài Tập Hàm Số Mũ
Nắm vững lý thuyết là bước đầu tiên, việc áp dụng vào giải các bài tập cụ thể mới là mục tiêu cuối cùng.
Dạng 1: Tìm hàm số khi biết đồ thị và ngược lại
Dạng 2: Tìm mối quan hệ giữa các cơ số khi biết đồ thị
Dạng 3: Tính đạo hàm của hàm số mũ
Hình ảnh tổng hợp các công thức đạo hàm quan trọng của hàm số mũ, bao gồm cả đạo hàm của hàm số mũ cơ bản và hàm số mũ hợp.
Dạng 4: Tính giới hạn của hàm số mũ
Hình ảnh liệt kê các công thức giới hạn thường dùng của hàm số mũ khi x tiến đến vô cùng hoặc một giá trị cụ thể.
Dạng 5: Tìm GTLN, GTNN của hàm số mũ trên một đoạn
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về tính chất của hàm số mũ. Chúc các bạn học tốt và đạt kết quả cao trong các kỳ thi!