Trong hình học Euclid, khái niệm về hai đường thẳng song song đóng vai trò then chốt, mở ra nhiều ứng dụng quan trọng. Bài viết này sẽ đi sâu vào “Tính Chất Hai đường Thẳng Song Song”, một chủ đề quan trọng trong chương trình toán học phổ thông, giúp bạn nắm vững kiến thức và áp dụng hiệu quả vào giải bài tập.
1. Định Nghĩa và Dấu Hiệu Nhận Biết Hai Đường Thẳng Song Song
Hai đường thẳng được gọi là song song nếu chúng nằm trên cùng một mặt phẳng và không có bất kỳ điểm chung nào. Kí hiệu: (a // b).
Để nhận biết hai đường thẳng song song, ta dựa vào các dấu hiệu sau:
- So le trong: Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau, thì hai đường thẳng đó song song.
- Đồng vị: Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau, thì hai đường thẳng đó song song.
- Trong cùng phía: Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau (tổng bằng 180 độ), thì hai đường thẳng đó song song.
Ví dụ:
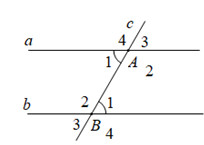
Góc A1 và B1 là hai góc so le trong bằng nhau, suy ra đường thẳng a song song với đường thẳng b.
2. Tiên Đề Ơ-Clit Về Đường Thẳng Song Song
Tiên đề Ơ-Clit khẳng định: “Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.” Đây là một trong những tiên đề cơ bản của hình học Euclid, là nền tảng để xây dựng nhiều định lý và bài toán liên quan đến đường thẳng song song.
3. Tính Chất Của Hai Đường Thẳng Song Song Khi Bị Cắt Bởi Một Đường Thẳng Thứ Ba
Đây là phần quan trọng nhất khi nói về “tính chất hai đường thẳng song song”. Khi hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba (gọi là cát tuyến), sẽ tạo ra các cặp góc có mối quan hệ đặc biệt:
- Các cặp góc so le trong bằng nhau: Các góc nằm ở vị trí so le trong sẽ có số đo bằng nhau.
- Các cặp góc đồng vị bằng nhau: Các góc nằm ở vị trí đồng vị sẽ có số đo bằng nhau.
- Các cặp góc trong cùng phía bù nhau: Tổng số đo của hai góc nằm ở vị trí trong cùng phía bằng 180 độ.
Minh họa:
Hai đường thẳng a và b song song với nhau, bị cắt bởi đường thẳng c, tạo thành các cặp góc có quan hệ đặc biệt.
Ví dụ cụ thể:
Nếu (a // b) thì:
- (widehat{A_1} = widehat{B_1}) (so le trong)
- (widehat{A_3} = widehat{B_1}) (đồng vị)
- (widehat{A_2} + widehat{B_1} = 180^o) (trong cùng phía)
4. Ứng Dụng của Tính Chất Hai Đường Thẳng Song Song
“Tính chất hai đường thẳng song song” được ứng dụng rộng rãi trong giải toán hình học, đặc biệt là các bài toán liên quan đến:
- Chứng minh hai đường thẳng song song: Dựa vào các dấu hiệu nhận biết (so le trong, đồng vị, trong cùng phía) để chứng minh hai đường thẳng song song.
- Tính số đo góc: Sử dụng các tính chất về góc so le trong, đồng vị, trong cùng phía để tính số đo của các góc chưa biết.
- Xây dựng các hình hình học: Tính chất này được sử dụng để vẽ các hình có tính chất đặc biệt như hình bình hành, hình thang cân,…
5. Các Dạng Bài Tập Thường Gặp và Phương Pháp Giải
-
Dạng 1: Chứng minh hai đường thẳng song song.
Phương pháp: Sử dụng các dấu hiệu nhận biết hai đường thẳng song song (so le trong, đồng vị, trong cùng phía).
-
Dạng 2: Tính số đo góc.
Phương pháp: Áp dụng tính chất của hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba (các góc so le trong bằng nhau, các góc đồng vị bằng nhau, các góc trong cùng phía bù nhau).
-
Dạng 3: Bài tập tổng hợp, kết hợp nhiều kiến thức.
Phương pháp: Phân tích kỹ đề bài, xác định các yếu tố đã cho và yêu cầu cần tìm. Kết hợp kiến thức về “tính chất hai đường thẳng song song” với các kiến thức hình học khác để giải bài toán.
6. Cách Vẽ Hai Đường Thẳng Song Song
Có nhiều cách để vẽ hai đường thẳng song song. Một trong những cách đơn giản nhất là sử dụng thước và êke.
Sử dụng thước và êke để vẽ hai đường thẳng song song một cách chính xác.
Kết luận:
Hiểu rõ “tính chất hai đường thẳng song song” là chìa khóa để giải quyết nhiều bài toán hình học. Nắm vững các định nghĩa, dấu hiệu nhận biết và các tính chất liên quan đến góc, bạn sẽ tự tin chinh phục các bài tập và ứng dụng kiến thức này vào thực tế.