Tính Chất Đường Cao Trong Tam Giác Vuông Cân: Bí Quyết Giải Toán Hình Học

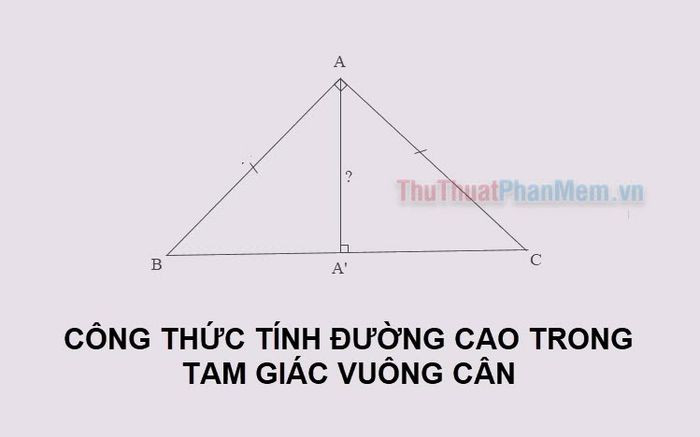
1. Đường cao trong tam giác vuông cân là gì?

Tam giác vuông cân là một dạng tam giác đặc biệt, kết hợp giữa tính chất vuông góc và cân bằng. Nó có một góc vuông (90 độ) và hai cạnh góc vuông có độ dài bằng nhau. Do đó, hai góc còn lại của tam giác vuông cân bằng nhau và mỗi góc có số đo là 45 độ.

Đường cao trong tam giác vuông cân là đoạn thẳng kẻ từ đỉnh góc vuông xuống cạnh huyền (cạnh đối diện góc vuông) và vuông góc với cạnh huyền. Đường cao này có tính chất đặc biệt là đồng thời là đường trung tuyến, chia cạnh huyền thành hai đoạn bằng nhau.

2. Các tính chất quan trọng của đường cao trong tam giác vuông cân

Đường cao xuất phát từ đỉnh góc vuông trong tam giác vuông cân mang những tính chất vô cùng đặc biệt và hữu ích trong việc giải toán hình học:

• Tính chất 1: Đường cao là đường trung tuyến: Đường cao này chia cạnh huyền thành hai đoạn thẳng có độ dài bằng nhau. Điểm giao giữa đường cao và cạnh huyền chính là trung điểm của cạnh huyền.

• Tính chất 2: Đường cao là đường phân giác: Đường cao này đồng thời là đường phân giác của góc vuông. Nó chia góc vuông thành hai góc bằng nhau, mỗi góc có số đo 45 độ.

• Tính chất 3: Đường cao là đường trung trực: Đường cao này vuông góc với cạnh huyền tại trung điểm của nó, do đó nó là đường trung trực của cạnh huyền.

• Tính chất 4: Đường cao tạo ra hai tam giác vuông cân nhỏ: Đường cao chia tam giác vuông cân ban đầu thành hai tam giác vuông cân nhỏ, bằng nhau và đồng dạng với tam giác ban đầu.

3. Ứng dụng tính chất đường cao để tính toán

Một trong những ứng dụng quan trọng nhất của đường cao trong tam giác vuông cân là khả năng tính toán độ dài của nó một cách dễ dàng dựa trên độ dài cạnh huyền hoặc cạnh góc vuông.

Công thức tính độ dài đường cao:

• Nếu biết độ dài cạnh huyền (ký hiệu là c), thì độ dài đường cao (ký hiệu là h) được tính theo công thức: h = c / 2

• Nếu biết độ dài cạnh góc vuông (ký hiệu là a), thì độ dài đường cao được tính theo công thức: h = a / √2 hoặc h = (a√2) / 2 (sau khi trục căn thức ở mẫu)

Ví dụ minh họa:

Cho tam giác ABC vuông cân tại A, cạnh huyền BC = 8cm. Tính độ dài đường cao AH.

Giải:

Áp dụng công thức: h = c / 2

Ta có: AH = BC / 2 = 8 / 2 = 4 cm

Vậy, độ dài đường cao AH là 4cm.

4. Bài tập vận dụng tính chất đường cao trong tam giác vuông cân

Để củng cố kiến thức, hãy cùng giải một số bài tập vận dụng sau:

Bài 1: Cho tam giác DEF vuông cân tại D, cạnh DE = DF = 5cm. Tính độ dài đường cao DK.

Bài 2: Cho tam giác MNP vuông cân tại M, đường cao MQ = 3√2 cm. Tính độ dài cạnh huyền NP.

Gợi ý:

• Bài 1: Sử dụng công thức h = a / √2
• Bài 2: Sử dụng công thức c = 2h

Nắm vững các tính chất và công thức liên quan đến đường cao trong tam giác vuông cân sẽ giúp bạn giải quyết các bài toán hình học một cách nhanh chóng và chính xác. Hãy luyện tập thường xuyên để thành thạo kỹ năng này!