Tam giác nội tiếp đường tròn là một khái niệm quan trọng trong hình học, đặc biệt là khi nghiên cứu về đường tròn. Bài viết này sẽ trình bày chi tiết về định nghĩa, các tính chất đặc biệt và ứng dụng của tam giác nội tiếp đường tròn, giúp bạn nắm vững kiến thức và giải quyết các bài toán liên quan một cách hiệu quả.
Định Nghĩa Tam Giác Nội Tiếp Đường Tròn
Tam giác được gọi là nội tiếp đường tròn nếu ba đỉnh của tam giác nằm trên đường tròn đó. Ngược lại, đường tròn đó được gọi là đường tròn ngoại tiếp tam giác.
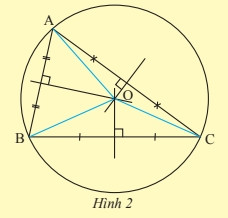
Hình ảnh minh họa tam giác nội tiếp đường tròn, với tâm đường tròn là giao điểm ba đường trung trực của tam giác.
Tính Chất Cơ Bản Của Tam Giác Nội Tiếp Đường Tròn
- Tâm đường tròn ngoại tiếp: Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
- Bán kính đường tròn ngoại tiếp: Bán kính của đường tròn ngoại tiếp bằng khoảng cách từ tâm đường tròn đến bất kỳ đỉnh nào của tam giác.
- Liên hệ giữa góc và cung: Trong một đường tròn, góc nội tiếp chắn một cung bằng một nửa số đo của góc ở tâm chắn cung đó.
Các Trường Hợp Đặc Biệt Của Tam Giác Nội Tiếp
1. Tam Giác Vuông Nội Tiếp Đường Tròn:
- Nếu một tam giác vuông nội tiếp đường tròn, thì cạnh huyền của tam giác trùng với đường kính của đường tròn.
- Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
- Bán kính của đường tròn ngoại tiếp tam giác vuông bằng một nửa độ dài cạnh huyền.
Ví dụ:
Hình ảnh minh họa tam giác vuông nội tiếp đường tròn, cạnh huyền là đường kính của đường tròn.
Trong tam giác ABC vuông tại A, nội tiếp đường tròn (O), BC là cạnh huyền thì O là trung điểm của BC và BC là đường kính của đường tròn (O).
2. Tam Giác Đều Nội Tiếp Đường Tròn:
- Tâm của đường tròn ngoại tiếp tam giác đều trùng với trọng tâm, trực tâm và giao điểm của ba đường phân giác của tam giác đó.
- Bán kính R của đường tròn ngoại tiếp tam giác đều cạnh a được tính theo công thức: .
Ví dụ:
Hình ảnh minh họa tam giác đều nội tiếp đường tròn, tâm đường tròn trùng với trọng tâm tam giác.
Trong tam giác đều ABC nội tiếp đường tròn (O), O đồng thời là trọng tâm, trực tâm, tâm đường tròn nội tiếp và ngoại tiếp của tam giác.
3. Tam Giác Cân Nội Tiếp Đường Tròn:
- Đường trung trực của cạnh đáy đồng thời là đường cao và đường phân giác của góc ở đỉnh.
- Tâm đường tròn ngoại tiếp nằm trên đường trung trực này.
Ứng Dụng Của Tam Giác Nội Tiếp Đường Tròn
Các Tính Chất Của Tam Giác Nội Tiếp đường Tròn được ứng dụng rộng rãi trong giải toán hình học, đặc biệt là các bài toán liên quan đến:
- Chứng minh các điểm cùng nằm trên một đường tròn.
- Xác định tâm và bán kính của đường tròn ngoại tiếp.
- Tính toán độ dài các đoạn thẳng và số đo các góc.
- Giải các bài toán thực tế liên quan đến thiết kế và xây dựng.
Bài Tập Vận Dụng
Bài 1: Cho tam giác ABC vuông tại A, cạnh BC = 10cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Giải:
Vì tam giác ABC vuông tại A, nên đường tròn ngoại tiếp tam giác có tâm là trung điểm của cạnh huyền BC. Do đó, bán kính đường tròn ngoại tiếp là R = BC/2 = 10/2 = 5cm.
Bài 2: Cho tam giác đều ABC cạnh a = 6cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Giải:
Bán kính đường tròn ngoại tiếp tam giác đều ABC là .
Kết Luận
Hiểu rõ các tính chất của tam giác nội tiếp đường tròn là chìa khóa để giải quyết nhiều bài toán hình học phức tạp. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và sâu sắc về chủ đề này. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng linh hoạt vào các bài toán thực tế.