Chóp tứ giác đều là một hình học không gian quan trọng, thường xuất hiện trong các bài toán và ứng dụng thực tế. Bài viết này sẽ cung cấp đầy đủ kiến thức về hình chóp tứ giác đều, từ định nghĩa, tính chất đến các công thức tính toán liên quan.
I. Định Nghĩa và Các Yếu Tố của Hình Chóp Tứ Giác Đều
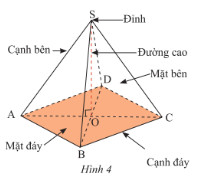
Hình chóp tứ giác đều là một loại hình chóp có những đặc điểm sau:
- Đáy: Là một hình vuông.
- Cạnh bên: Bốn cạnh bên có độ dài bằng nhau.
- Mặt bên: Bốn mặt bên là các tam giác cân bằng nhau, có chung một đỉnh.
- Đường cao: Chân đường cao của hình chóp trùng với giao điểm của hai đường chéo của hình vuông đáy.
II. Các Tính Chất Quan Trọng của Hình Chóp Tứ Giác Đều
Hình chóp tứ giác đều sở hữu những tính chất hình học đặc trưng, giúp ta dễ dàng nhận biết và tính toán các thông số liên quan:
- Tính đối xứng: Có trục đối xứng là đường thẳng đi qua đỉnh và tâm của đáy (giao điểm hai đường chéo).
- Các mặt bên bằng nhau: Bốn mặt bên là các tam giác cân đồng dạng.
- Các cạnh bên bằng nhau: Độ dài các cạnh bên là như nhau.
- Đường cao: Đường cao hạ từ đỉnh xuống đáy vuông góc với đáy tại tâm của hình vuông đáy.
III. Công Thức Tính Diện Tích và Thể Tích Hình Chóp Tứ Giác Đều
1. Diện tích xung quanh
Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích của bốn mặt bên. Để tính diện tích xung quanh, ta sử dụng công thức:
(S_{xq} = p.d)
Trong đó:
- (S_{xq}): Diện tích xung quanh của hình chóp.
- (p): Nửa chu vi đáy (nửa chu vi hình vuông).
- (d): Độ dài trung đoạn (chiều cao của một mặt bên hạ từ đỉnh).
2. Thể tích
Thể tích của hình chóp tứ giác đều được tính bằng một phần ba diện tích đáy nhân với chiều cao của hình chóp:
(V = frac{1}{3}{S_{đáy}}.h)
Trong đó:
- (V): Thể tích của hình chóp.
- ({S_{đáy}}): Diện tích đáy (diện tích hình vuông).
- (h): Chiều cao của hình chóp (khoảng cách từ đỉnh đến mặt đáy).
Ví dụ:
Cho hình chóp tứ giác đều có cạnh đáy bằng 6cm và chiều cao bằng 16cm. Thể tích của hình chóp là:
(V = frac{1}{3}.6.6.16 = 192 (cm^3))
IV. Bài Tập Vận Dụng
Để hiểu rõ hơn về hình chóp tứ giác đều và cách áp dụng các công thức, hãy cùng xem xét một số bài tập sau:
Bài 1: Tính diện tích xung quanh của một hình chóp tứ giác đều, biết cạnh đáy bằng 5cm và trung đoạn bằng 8cm.
Giải:
Nửa chu vi đáy là: (p = frac{4 times 5}{2} = 10 (cm))
Diện tích xung quanh là: (S_{xq} = p times d = 10 times 8 = 80 (cm^2))
Bài 2: Một hình chóp tứ giác đều có thể tích là (100 cm^3) và chiều cao là 12cm. Tính diện tích đáy của hình chóp.
Giải:
Ta có: (V = frac{1}{3} times S{đáy} times h)
Suy ra: (S{đáy} = frac{3 times V}{h} = frac{3 times 100}{12} = 25 (cm^2))
Bài 3: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = a và chiều cao SO = h. Tính thể tích của hình chóp.
Giải:
Diện tích đáy là (S_{ABCD} = a^2)
Thể tích hình chóp là: (V = frac{1}{3} times a^2 times h)
V. Ứng Dụng Thực Tế
Hình chóp tứ giác đều không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng trong thực tế, ví dụ như:
- Kiến trúc: Các công trình kiến trúc như mái nhà, tháp, hoặc các công trình trang trí có thể có dạng hình chóp tứ giác đều.
- Thiết kế: Các vật dụng hàng ngày như lều trại, hộp đựng đồ, hoặc các sản phẩm trang trí có thể được thiết kế dựa trên hình dạng này.
VI. Kết Luận
Hiểu rõ về Tính Chất Chóp Tứ Giác đều giúp chúng ta giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả hơn. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về hình chóp tứ giác đều, từ định nghĩa, tính chất, công thức tính toán đến các ứng dụng thực tế.