Bài viết này sẽ giúp bạn nắm vững kiến thức về Tính Chất Các Hình học phẳng cơ bản, bao gồm hình thang cân, hình bình hành, hình chữ nhật, hình thoi và hình vuông. Chúng ta sẽ đi sâu vào định nghĩa, tính chất và dấu hiệu nhận biết của từng loại hình, kèm theo các ví dụ minh họa để bạn dễ dàng áp dụng vào giải bài tập.
I. Hình Thang Cân: Tính Chất và Dấu Hiệu Nhận Biết
1. Định nghĩa: Hình thang cân là một hình thang đặc biệt, nổi bật với hai góc kề một đáy bằng nhau.
2. Tính chất:
- Hai góc kề một đáy bằng nhau.
- Hai đường chéo có độ dài bằng nhau.
3. Dấu hiệu nhận biết:
- Hình thang có hai góc kề một đáy bằng nhau.
- Hình thang có hai đường chéo bằng nhau.
4. Ví dụ minh họa:
Ví dụ 1: Cho hình thang ABCD (AB // CD) có góc ACD = góc BDC. Chứng minh rằng ABCD là hình thang cân.
(Chứng minh tương tự bài gốc)
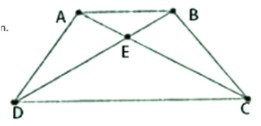
Ví dụ 2: Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh EA = EB, EC = ED.
Hình thang cân ABCD với E là giao điểm hai đường chéo AC và BD, chứng minh EA=EB và EC=ED
II. Hình Bình Hành: Đặc Điểm và Cách Nhận Biết
1. Định nghĩa: Hình bình hành là một tứ giác mà các cạnh đối song song với nhau.
2. Tính chất:
- Các cạnh đối bằng nhau.
- Các góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
3. Dấu hiệu nhận biết:
- Tứ giác có các cạnh đối song song.
- Tứ giác có các cạnh đối bằng nhau.
- Tứ giác có hai cạnh đối song song và bằng nhau.
- Tứ giác có các góc đối bằng nhau.
- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành ABCD: Các cạnh đối AB // CD và AD // BC, các cạnh đối bằng nhau AB = CD và AD = BC, hai đường chéo AC và BD cắt nhau tại trung điểm O
III. Hình Chữ Nhật: Tính Chất Đặc Trưng
1. Định nghĩa: Hình chữ nhật là một tứ giác có bốn góc vuông.
2. Tính chất:
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
- Sở hữu tất cả các tính chất của hình thang cân và hình bình hành.
3. Dấu hiệu nhận biết:
- Tứ giác có ba góc vuông.
- Hình thang cân có một góc vuông.
- Hình bình hành có một góc vuông.
- Hình bình hành có hai đường chéo bằng nhau.
IV. Hình Thoi: Tính Chất và Ứng Dụng
1. Định nghĩa: Hình thoi là một tứ giác đặc biệt, có bốn cạnh bằng nhau.
2. Tính chất:
- Hai đường chéo vuông góc với nhau.
- Hai đường chéo là các đường phân giác của các góc của hình thoi và cắt nhau tại trung điểm của mỗi đường.
- Sở hữu tất cả các tính chất của hình bình hành.
3. Dấu hiệu nhận biết:
- Tứ giác có bốn cạnh bằng nhau.
- Hình bình hành có hai cạnh kề bằng nhau.
- Hình bình hành có hai đường chéo vuông góc với nhau.
- Hình bình hành có một đường chéo là đường phân giác của một góc.
4. Bài tập minh họa:
Ví dụ 1: (Như bài gốc)
Ví dụ 2: Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Đường thẳng AH cắt EF tại D, cắt BC tại G. Gọi M và N lần lượt là hình chiếu của G trên AB và AC. Chứng minh rằng tứ giác DNGM là hình thoi.
Tam giác ABC cân tại A với đường cao BE và CF, chứng minh tứ giác DNGM là hình thoi khi G là hình chiếu của AH trên BC, và M, N là hình chiếu của G trên AB, AC.
V. Hình Vuông: Tổng Hợp Các Tính Chất
1. Định nghĩa: Hình vuông là một tứ giác có bốn góc vuông và bốn cạnh bằng nhau. Nói cách khác, hình vuông vừa là hình chữ nhật, vừa là hình thoi.
2. Tính chất:
- Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
3. Dấu hiệu nhận biết:
- Hình chữ nhật có hai cạnh kề bằng nhau.
- Hình chữ nhật có hai đường chéo vuông góc với nhau.
- Hình chữ nhật có một đường chéo là đường phân giác của một góc.
- Hình thoi có một góc vuông.
- Hình thoi có hai đường chéo bằng nhau.